Решебник по алгебре 9 класс Мерзляк Задание 468
Задание 468



\[\boxed{\text{468\ (468).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
\[1)\ \left\{ \begin{matrix} x^{2} - 12xy + 36y^{2} = 36 \\ x + 6y = 8\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ \ \ \ }\]
\[\left\{ \begin{matrix} (x - 6y)^{2} = 36 \\ x + 6y = 8\ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} (x - 6y)^{2} = 36 \\ x = 8 - 6y\ \ \ \ \ \ \ \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ \ \ }\]
\[\left\{ \begin{matrix} (8 - 12y)^{2} = 36 \\ x = 8 - 6y\ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ \ \ }\]
\[\left\{ \begin{matrix} 64 - 192y + 144y^{2} - 36 = 0 \\ x = 8 - 6y\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]
\[144y^{2} - 192y + 28 = 0\ \ \ \ \ \ \ |\ :4\]
\[36y^{2} - 48y + 7 = 0\]
\[D = 1296\]
\[y_{1,2} = \frac{48 \pm 36}{72}\]
\[\left\{ \begin{matrix} y = \frac{7}{6} \\ x = 1 \\ \end{matrix} \right.\ \ \ \ или\ \ \ \left\{ \begin{matrix} y = \frac{1}{6} \\ x = 7 \\ \end{matrix} \right.\ \]
\[Ответ:\left( 1;\frac{7}{6} \right),\ \left( 7;\frac{1}{6} \right).\]
\[2)\ \left\{ \begin{matrix} y^{2} - 2xy = 32\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ x^{2} + 6xy + 9y^{2} = 100 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ \ }\]
\[\text{\ \ }\left\{ \begin{matrix} y^{2} - 2xy = 32 \\ (x + 3y)^{2} = 100 \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} y^{2} - 2xy = 32 \\ x + 3y = 10 \\ \end{matrix} \right.\ \ \ \ \ \ \ \ \ \ \ \ \ \ или\ \ \ \ \ \ \ \ \ \ \ \ \]
\[\ \left\{ \begin{matrix} y^{2} - 2xy = 32 \\ x + 3y = - 10 \\ \end{matrix} \right.\ \]


\[3)\ \left\{ \begin{matrix} x^{2} + y^{2} = 25\ \ \ \\ xy = 12\ \ \ \ \ \ \ | \cdot 2 \\ \end{matrix} \right.\ + \ \ \ \ \ \ \ \ \ \ \ \ \]
\[\left\{ \begin{matrix} x^{2} + y^{2} + 2xy = 49 \\ xy = 12\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} (x + y)^{2} = 49 \\ xy = 12\ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} x + y = 7 \\ xy = 12\ \ \\ \end{matrix} \right.\ \ \ \ \ или\ \ \ \ \left\{ \begin{matrix} x + y = - 7 \\ xy = 12\ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} x = 7 - y\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ 7y - y^{2} - 12 = 0 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }\]
\[\text{\ \ \ }\left\{ \begin{matrix} x = - 7 - y\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ - 7y - y^{2} - 12 = 0 \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} y = 4 \\ x = 3 \\ \end{matrix} \right.\ \ \ \ или\ \ \ \left\{ \begin{matrix} y = - 4 \\ x = - 3 \\ \end{matrix} \right.\ \ \ \ \ или\ \ \]
\[\ \left\{ \begin{matrix} y = 3 \\ x = 4 \\ \end{matrix} \right.\ \ \ \ \ или\ \ \ \left\{ \begin{matrix} y = - 3 \\ x = - 4 \\ \end{matrix} \right.\ \]
\[Ответ:(3;4),\ (4;3),\ ( - 3;\ - 4),\ \]
\[( - 4;\ - 3).\]
\[4)\ \left\{ \begin{matrix} 9x^{2} + y^{2} = 10 \\ xy - 1\ \ \ \ \ \ | \cdot 6\ \ \\ \end{matrix} + \right.\ \text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }\]
\[\left\{ \begin{matrix} 9x^{2} + y^{2} + 6xy = 4 \\ xy = - 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} (3x + y)^{2} = 4 \\ xy = - 1\ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} 3x + y = 2 \\ xy = - 1\ \ \ \\ \end{matrix} \right.\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ или\ \ \ \ \ \ \ \ \ \ \ \ \ \]
\[\ \left\{ \begin{matrix} 3x + y = - 2 \\ xy = - 1\ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} y = 2 - 3x\ \ \ \ \ \ \ \ \ \ \ \ \ \\ 2x - 3x^{2} + 1 = 0 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }\]
\[\text{\ \ \ }\left\{ \begin{matrix} y = - 2 - 3x\ \ \ \ \ \ \ \ \ \ \ \ \ \\ - 2x - 3x^{2} + 1 = 0 \\ \end{matrix} \right.\ \]



\[\boxed{\text{468.\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
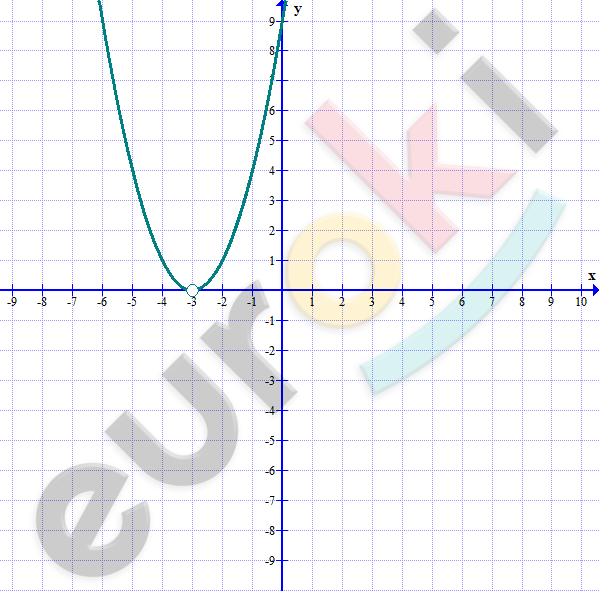
\[1)\ y = \frac{(x + 3)^{3}}{(x + 3)};\ \ x \neq - 3\]
\[y = (x + 3)^{2}\]
\[a = 1 > 0 - ветви\ вверх;\]
\[( - 3;0) - вершина\ параболы\ \]
\[(выколотая\ точка).\]
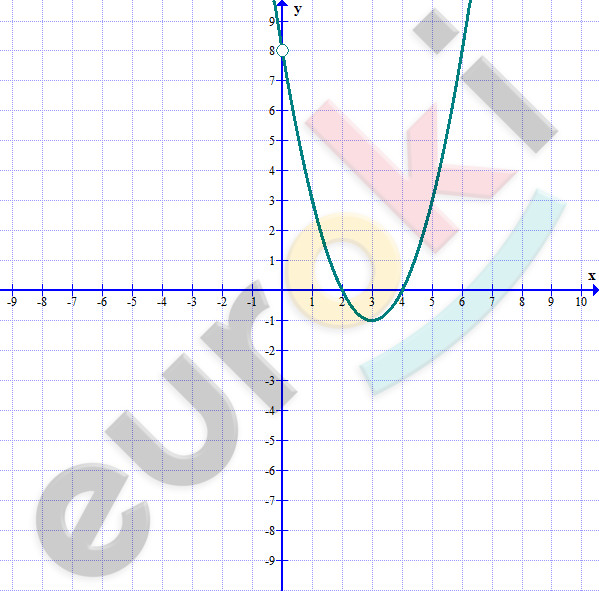
\[2)\ y = \frac{x^{3} - 6x^{2} + 8x}{x};\ \ \ x \neq 0\]
\[y = x^{2} - 6x + 8\]
\[a = 1 > 0 - ветви\ вверх.\]
\[x_{0} = \frac{6}{2} = 3;\]
\[y_{0} = 9 - 18 + 8 = - 1.\ \ \]
\[(3;\ - 1) - вершина\ параболы.\]
\[y = 0:\ \ \]
\[x^{2} - 6x + 8 = 0\]
\[x_{1} + x_{2} = 6,\ \ x_{1} = 2\]
\[x_{1}x_{2} = 8,\ \ x_{2} = 4\]
\[(2;0),\ \ (4;0).\]
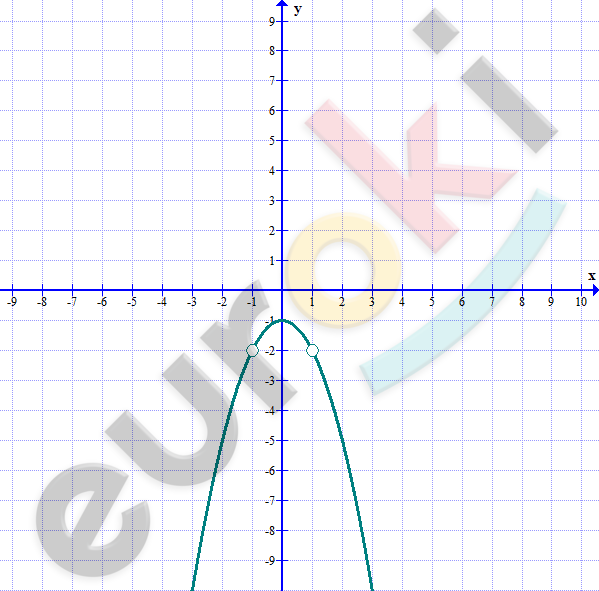
\[3)\ y = \frac{x^{4} - 1}{1 - x^{2}}\]
\[y = \frac{(x^{2} - 1)(x^{2} + 1)}{(1 - x^{2})};\ \ x \neq \pm 1\]
\[y = - \left( x^{2} + 1 \right)\]
\[a = - 1 < 0 - ветви\ вверх;\]
\[(0; - 1) - вершина\ параболы.\]