Решебник по алгебре 9 класс Мерзляк Задание 348

 

\[\boxed{\text{348\ (348).\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[f(x) = - x^{2} - 6x - 5\]

\[x_{0} = \frac{6}{- 2} = - 3;\]

\[y_{0} = - 9 + 18 - 5 = 4.\]

\[Ox:\ \text{\ \ \ }\]

\[- x^{2} - 6x - 5 = 0\]

\[x_{1} + x_{2} = - 6,\ \ x_{1}x_{2} = 5,\ \ \]

\[x_{1} = - 1,\ \ x_{2} = - 5\]

\[( - 1;0),\ \ ( - 5;0).\]

\[\text{Oy}:\ \ y = - 5,\ \ \ (0;\ - 5).\]

\[1)\ E(y) = ( - \infty;4\rbrack.\]

\[2)\ функция\ возрастает\ на\ \]

\[промежутке\ ( - \infty;\ - 3\rbrack.\]

\[3)\ f(x) > 0\ при\ x \in ( - 5;\ - 1).\]

\[\boxed{\text{348.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[Пусть\ x\ \frac{км}{ч} - скорость\ \]

\[мотоциклиста\ до\ задержки,\ \]

\[тогда\ \]

\[(x + 12)\ \frac{км}{ч} - новая\ \]

\[скорость\ мотоциклиста.\ \]

\[Тогда\ (120 - 2x)\ км -\]

\[путь\ мотоциклиста\ с\ \]

\[первоначальной\ скоростью,\ \]

\[а\frac{120 - 2x}{x}\ ч -\]

\[время,\ на\ дорогу\ до\ задержки.\ \]

\[Значит,\frac{120 - 2x}{x + 12}\ ч -\]

\[время\ на\ дорогу\ \]

\[после\ задержки.\ По\ условию\ \]

\[известно,\ что\ задержка\ \]

\[составила\ \]

\[6\ мин = \frac{1}{10}\ ч.\]

\[Составляем\ уравнение:\]

\[\frac{120 - 2x}{x} - \frac{120 - 2x}{x + 12} = \frac{1}{10}\]

\[10 \cdot (x + 12) \cdot (120 - 2x) -\]

\[- 10x \cdot (120 - 2x) -\]

\[- x \cdot (x + 12) = 0\]

\[(10x + 120) \cdot (120 - 2x) -\]

\[- 1200x + 20x^{2} - x^{2} - 12x = 0\]

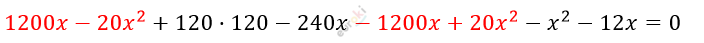
\[- x^{2} - 252x + 14400 = 0\ | \cdot ( - 1)\]

\[x^{2} + 252x - 14400 = 0\]

\[D = 63504 + 57600 = 121\ 104\]

\[x = \frac{- 252 \pm 348}{2}\]

\[x = 48\]

\[x = - 300 - не\ удовлетворяет.\]

\[48\frac{км}{ч} - первоначальная\ \]

\[скорость.\]

\[{48 + 12 = 60\ \left( \frac{км}{ч} \right) - скорость\ }{мотоциклиста\ после\ задержки.}\]

\[Ответ:60\ \frac{км}{ч}\text{.\ \ }\]