Решебник по алгебре 9 класс Мерзляк Задание 278
Задание 278



\[\boxed{\text{278\ (278).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
Пояснение.

Решение.
\[Пусть\ x_{1}\ и\ x_{2} - любые\ \]
\[значения\ x\ на\ промежутках\ \]
\[( - \infty;0)\ и\ (0; + \infty)\ и\]
\[x_{1} < x_{2};\ k > 0.\]
\[Тогда\ \frac{k}{x_{1}} > \frac{k}{x_{2}}\ на\ промежутке\ \]
\[(0;\ + \infty)\ получаем,\ \]
\[что\ x_{1} < x_{2};\ y_{1} > y_{2}.\]
\[Следовательно,\ функция\ \]
\[убывает\ на\ (0;\ + \infty),\]
\[\ аналогично\ убывает\ на\]
\[( - \infty;0)\text{.\ }\]
\[Пусть\ x_{1}\ и\ x_{2} - любые\ \]
\[значения\ x\ на\ промежутках\ \]
\[( - \infty;0)\ и\ (0;\ + \infty)\]
\[и\ x_{1} < x_{2};\ k < 0,\ то\ \frac{k}{x_{1}} < \frac{k}{x_{2}}\ \]
\[на\ промежутках\ (0;\ + \infty)\ и\ \]
\[( - \infty;0).\]
\[Получаем,\ что\ x_{1} < x_{2};\ y_{1} < y_{2}.\]
\[Следовательно,\ функция\ \]
\[возрастает.\ \]

\[\boxed{\text{278.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
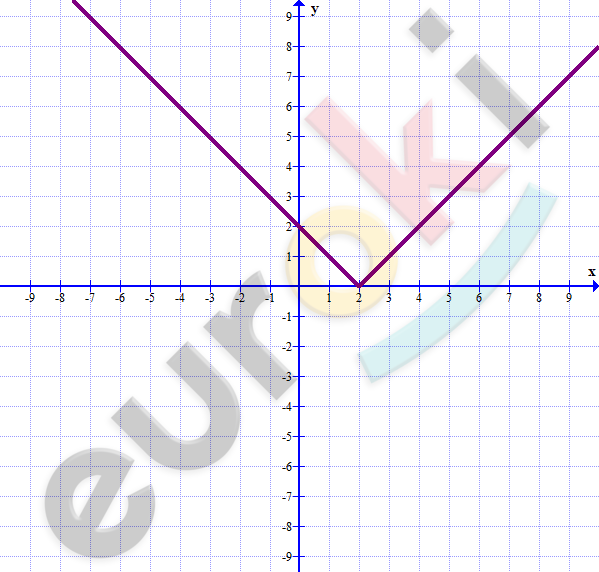
\[1)\ y = |x - 2|\]
\[y = \left\{ \begin{matrix} x - 2;\ \ \ если\ x \geq 2 \\ - x + 2;если\ x < 2 \\ \end{matrix} \right.\ \text{\ \ \ }\]
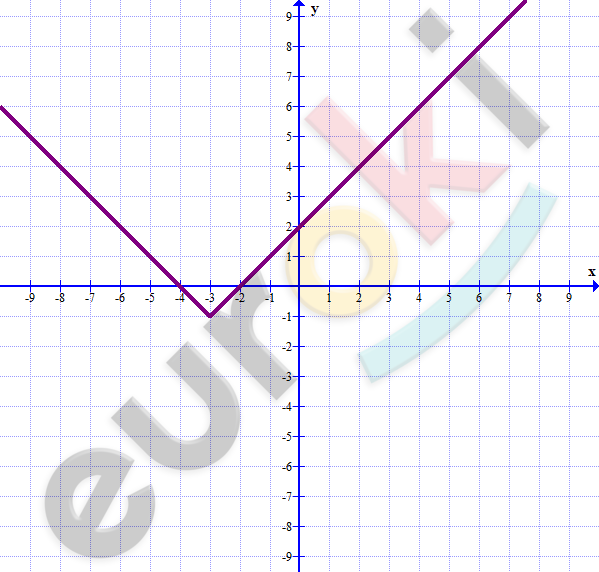
\[2)\ y = |x + 3| - 1\]
\[x \geq - 3:\]
\[y = x + 3 - 1 = x + 2\]
| \[x\] | \[0\] | \[1\] |
|---|---|---|
| \[y\] | \[2\] | \[3\] |
\[x < - 3:\]
\[y = - x - 3 - 1 = - x - 4\ \]
| \[x\] | \[- 1\] | \[- 2\] |
|---|---|---|
| \[y\] | \[- 3\] | \[- 2\] |
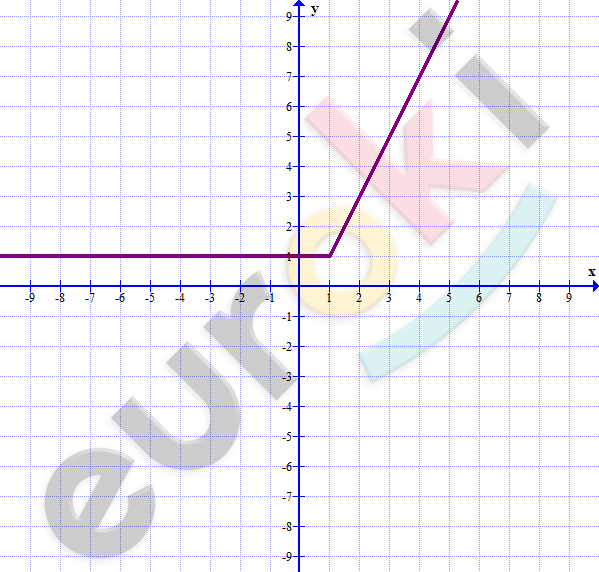
\[3)\ y = |x - 1| + x\]
\[x \geq 1:\]
\[y = x - 1 + x = 2x - 1\]
| \[x\] | \[0\] | \[1\] |
|---|---|---|
| \[y\] | \[- 1\] | \[1\] |
\[x < 1:\]
\[y = - x + 1 + x = 1\]
 \(\ \)
\(\ \)




