Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по алгебре 9 класс Мерзляк Задание 177
Задание 177
\[\boxed{\text{177\ (177).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
Пояснение.
\[\mathbf{Числовые\ промежутки.}\]
Решение.
\[\left\{ \begin{matrix} x > - 1 \\ x \leq 6\ \ \ \\ \end{matrix} \right.\ \]
\[x \in ( - 1;6\rbrack\]
\[Ответ:рисунок\ б).\]
\[\boxed{\text{177.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
\[1)\ \left\{ \begin{matrix} x + y - xy = 1 \\ \text{xy}(x + y) = 20 \\ \end{matrix} \right.\ \]
\[Пусть\ xy = a;\ \ x + y = b,\ тогда:\]
\[\left\{ \begin{matrix} b - a = 1 \\ ab = 20\ \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ }\]
\[\ \left\{ \begin{matrix} b = 1 + a\ \ \ \ \ \ \ \ \ \ \ \\ a + a^{2} - 20 = 0 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }\]
\[\left\{ \begin{matrix} b = - 4 \\ a = - 5 \\ \end{matrix} \right.\ \ \ \ или\ \ \ \left\{ \begin{matrix} b = 5 \\ a = 4 \\ \end{matrix} \right.\ \]
\[a_{1} + a_{2} = - 1\]
\[a_{1}a_{2} = - 20\]
\[\left\{ \begin{matrix} a_{1} = - 5 \\ a_{2} = 4\ \ \ \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} xy = - 5\ \ \ \ \ \\ x + y = - 4 \\ \end{matrix} \right.\ \ \ \ или\ \ \ \ \ \ \ \ \ \ \ \ \ \]
\[\text{\ \ }\left\{ \begin{matrix} xy = 4\ \ \ \ \ \\ x + y = 5 \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} x = 1\ \ \ \ \\ y = - 5 \\ \end{matrix} \right.\ \ \ \ или\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \]
\[\ \left\{ \begin{matrix} x = 4 \\ y = 1 \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} x = - 5 \\ y = 1\ \ \ \ \\ \end{matrix} \right.\ \ \ \ или\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \]
\[\text{\ \ }\left\{ \begin{matrix} x = 1 \\ y = 4 \\ \end{matrix} \right.\ \text{\ \ }\]
\[Ответ:(1; - 5),\ (1;4),\ \]
\[( - 5;1),\ (4;1).\]
\[2)\ \left\{ \begin{matrix} \frac{y}{x} - \frac{x}{y} = \frac{21}{10} \\ x + y = 3 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ \ \ }\]
\[\ \left\{ \begin{matrix} \frac{y}{x} - \frac{x}{y} = \frac{21}{10} \\ x = 3 - y\ \\ \end{matrix} \right.\ \]
\[\frac{y}{3 - y} - \frac{3 - y}{y} - \frac{21}{10} = 0\]
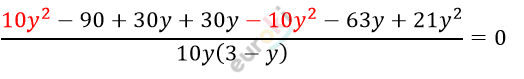
\[21^{2} - 3y - 90 = 0\ \ \ |\ :3,\ \ \]
\[y \neq 3\]
\[7y^{2} - y - 30 = 0\]
\[D = 1 + 840 = 841\]
\[y = \frac{1 + 29}{14} = \frac{15}{7}\]
\[y = \frac{1 - 29}{14} = - 2\]
\[\left\{ \begin{matrix} x = \frac{6}{7}\text{\ \ } \\ y = \frac{15}{7} \\ \end{matrix} \right.\ \ \ \ или\ \ \ \left\{ \begin{matrix} x = 5\ \ \ \\ y = - 2 \\ \end{matrix} \right.\ \]
\[Ответ:\left( \frac{6}{7};\frac{15}{7} \right);\ (5;\ - 2).\]
\[3)\ \left\{ \begin{matrix} \frac{x}{y} + \frac{6y}{x} = 5\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ x^{2} + 4xy - 3y^{2} = 18 \\ \end{matrix} \right.\ \]
\[Пусть\frac{x}{y} = a,\frac{y}{x} = \frac{1}{a}\]
\[a + \frac{6}{a} = 5\]
\[a^{2} + 6 - 5a = 0\]
\[a_{1} + a_{2} = 5\]
\[a_{1}a_{2} = 6\]
\[\left\{ \begin{matrix} a_{1} = 2 \\ a_{2} = 3 \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} \frac{x}{y} = 2\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ x^{2} + 4xy - 3y^{2} - 18 = 0 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ \ \ }\]
\[\ \left\{ \begin{matrix} x = 2y\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ 4y^{2} + 8y^{2} - 3y^{2} - 18 = 0 \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} x = 2y \\ 9y^{2} = 18 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ }\left\{ \begin{matrix} x = 2y \\ y^{2} = 2 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ }\]
\[\ \left\{ \begin{matrix} x = 2y\ \ \ \\ y = \pm \sqrt{2} \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ \ }\left\{ \begin{matrix} x = 2\sqrt{2} \\ y = \sqrt{2} \\ \end{matrix} \right.\ \ \ \ или\ \ \]
\[\ \left\{ \begin{matrix} x = - 2\sqrt{2} \\ y = - \sqrt{2} \\ \end{matrix} \right.\ \ \]
\[\left\{ \begin{matrix} \frac{x}{y} = 3\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ x^{2} + 4xy - 3y^{2} - 18 = 0 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ }\]
\[\text{\ \ }\left\{ \begin{matrix} x = 3y\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ 9y^{2} + 12y^{2} - 3y^{2} - 18 = 0 \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} x = 3y\ \ \ \ \ \ \\ 18y^{2} = 18 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ }\left\{ \begin{matrix} x = 3y \\ y^{2} = 1 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ \ }\]
\[\ \left\{ \begin{matrix} x = 3y \\ y = \pm 1 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ \ }\left\{ \begin{matrix} x = 3 \\ y = 1 \\ \end{matrix} \right.\ \ \ \ \ или\ \ \ \]
\[\left\{ \begin{matrix} x = - 3 \\ y = - 1 \\ \end{matrix} \right.\ \]
\[Ответ:\left( 2\sqrt{2};\sqrt{2} \right),\ \left( - 2\sqrt{2};\ - \sqrt{2} \right),\ \]
\[(3;1),\ ( - 3;\ - 1).\]
\[4)\ \left\{ \begin{matrix} \frac{1}{x} + \frac{1}{y} = \frac{5}{6} \\ \frac{1}{x} - \frac{1}{y} = \frac{1}{6} \\ \end{matrix} \right.\ \]
\[Пусть\ \frac{1}{x} = a,а\ \ \ \frac{1}{y} = b,\ тогда:\ \]
\[\left\{ \begin{matrix} a + b = \frac{5}{6} \\ a - b = \frac{1}{6} \\ \end{matrix}\ ( - ) \right.\ \text{\ \ \ \ \ \ \ \ \ }\]
\[\text{\ \ \ }\left\{ \begin{matrix} 2b = \frac{2}{3}\text{\ \ \ \ \ \ } \\ a - b = \frac{1}{6} \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ }\left\{ \begin{matrix} b = \frac{1}{3} \\ a = \frac{1}{2} \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} \frac{1}{x} = \frac{1}{2} \\ \frac{1}{y} = \frac{1}{3} \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ \ \ }\left\{ \begin{matrix} x = 2 \\ y = 3 \\ \end{matrix} \right.\ \]
\[Ответ:(2;3).\]
