Решебник по алгебре 9 класс Мерзляк Задание 150

 

\[\boxed{\text{150\ (150).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[Пусть\ наши\ последовательные\ \]

\[натуральные\ числа,\ кратные\ 5:\]

\[5x,\ 5x + 5,\ 5x + 10.\]

\[Их\ сумма\ не\ больше\ 100\ \]

\[(по\ условию).\]

\[Составим\ неравенство:\]

\[5x + 5x + 5 + 5x + 10 \leq 100\]

\[15x \leq 85\]

\[x \leq 5\frac{2}{3}\]

\[x_{\max} = 5.\]

\[Наши\ числа:\ \ \ 25,\ 30,\ 35.\]

\[Ответ:25,\ 30,\ 35.\]

\[\boxed{\mathbf{150.\ }Еуроки\ - \ ДЗ\ без\ мороки}\]

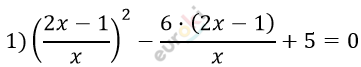
\[\left\{ \begin{matrix} \frac{2x - 1}{x} = t\ \ \ \ \ \ \ \\ t^{2} - 6t + 5 = 0 \\ \end{matrix} \right.\ \]

\[t_{1} + t_{2} = 6,\ \ t_{1} \cdot t_{2} = 5,\ \ \]

\[t_{1} = 5,\ \ t_{2} = 1\]

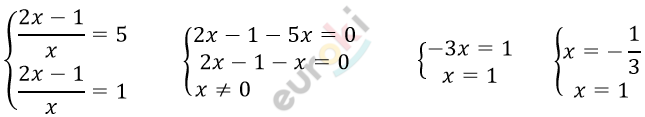
\[Ответ:\ x = - \frac{1}{3};\ \ x = 1.\]

\[2)\ \frac{3x - 1}{x + 1} + \frac{x + 1}{3x - 1} = 3\frac{1}{3}\]

\[\left\{ \begin{matrix} \frac{3x - 1}{x + 1} = t\ \ \ \ \ \ \\ t + \frac{1}{t} - \frac{10}{3} = 0 \\ \end{matrix} \right.\ \]

\[3t^{2} + 3 - 10t = 0\]

\[D = 100 - 36 = 64\]

\[x_{1} = \frac{10 - 8}{6} = \frac{1}{3}\]

\[x_{2} = \frac{10 + 8}{6} = 3\]

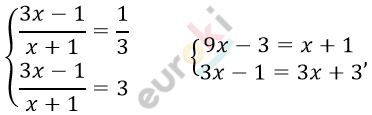
\[\ 8x = 4\ \]

\[\ x = 0,5\]

\[Ответ:x = 0,5.\]