Решебник по алгебре 8 класс Мерзляк ФГОС Задание 849

 

\[\boxed{\mathbf{849\ (849).\ }Еуроки\ - \ ДЗ\ без\ мороки}\]

\[1)\ \frac{8}{x} - \frac{5}{y} = \frac{8y - 5x}{\text{xy}}\]

\[2)\ \frac{7}{\text{ab}} + \frac{5}{b} = \frac{7 + 5a}{\text{ab}}\]

\[3)\ \frac{5}{24xy} - \frac{7}{18xy} = \frac{15 - 28}{72xy} =\]

\[= \frac{- 13}{72xy}\]

\[4)\ \frac{5b^{2} - 8b + 1}{a^{2}b^{2}} - \frac{2b - 1}{a^{2}b} =\]

\[= \frac{5b^{2} - 8b + 1 - 2b^{2} + b}{a^{2}b^{2}} =\]

\[= \frac{3b² - 7b + 1}{a²b²}\]

\[\boxed{\mathbf{8}\mathbf{4}\mathbf{9}\mathbf{\text{.\ }}Еуроки\ - \ ДЗ\ без\ мороки}\]

\[Пусть\ x\frac{км}{ч} - скорость\ \]

\[течения\ реки,\ \]

\[тогда\ (12 - x)\frac{км}{ч} -\]

\[скорость\ катера\ против\ \]

\[течения\ реки.\ Значит,\ плот\ \]

\[плыл\ \frac{14}{x}\ ч,\]

\[а\ катер\ - \frac{32 - 14}{12 - x}\ ч.\ \]

\[По\ условию\ изветстно,\ \]

\[что\ плот\ отплыл\ \]

\[на\ 2\ ч\ 40\ мин = 2\frac{2}{3} = \frac{8}{3}\ ч\ \]

\[раньше.\]

\[Составляем\ уравнение:\]

\[\frac{14}{x} - \frac{18}{12 - x} = \frac{8}{3}\]

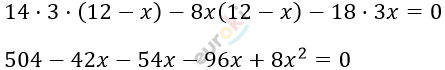
\[8x^{2} - 192x + 504 = 0\ \ \ \ |\ :8\]

\[x^{2} - 24x + 63 = 0\]

\[x_{1} + x_{2} = 24,\ \ \text{\ x}_{1}x_{2} = 63\]

\[x_{1} = 3\]

\[x_{2} = 21\]

\[Проверим:12 - 3 = 9\ \left( \frac{км}{ч} \right).\]

\[12 - 21 = - 9\ \left( \frac{км}{ч} \right) - не\ \]

\[удовлетворяет\ условию.\ \]

\[3\ \frac{км}{ч} - скорость\ течения\ \]

\[реки.\]

\[Ответ:3\frac{км}{ч}.\]