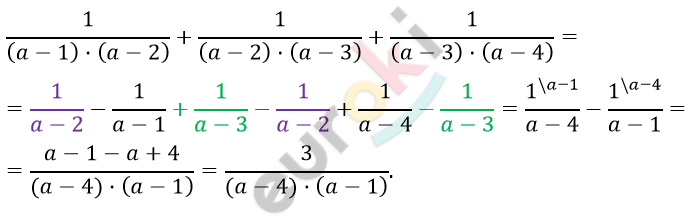Решебник по алгебре 8 класс Мерзляк Задание 126

\[\boxed{\text{126\ (126).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

Решение.

\[\frac{1}{(a - b) \cdot (a - c)} -\]

\[- \frac{1}{(a - b) \cdot (b - c)} +\]

\[+ \frac{1}{(c - a) \cdot (c - b)} = 0\]

\[Упростим\ левую\ часть\ \]

\[равенства:\]

\[\frac{1^{\backslash b - c}}{(a - b) \cdot (a - c)} -\]

\[- \frac{1^{\backslash a - c}}{(a - b) \cdot (b - c)} +\]

\[+ \frac{1^{\backslash a - b}}{(a - c) \cdot (b - c)} = 0\]

\[\frac{(b - c) - (a - c) + (a - b)}{(a - b) \cdot (a - c) \cdot (b - c)} = 0\]

\[\frac{b - c - a + c + a - b}{(a - b) \cdot (a - c) \cdot (b - c)} = 0\]

\[\frac{0}{(a - b) \cdot (a - c) \cdot (b - c)} = 0\]

\[0 = 0.\ \]