Решебник по алгебре 8 класс Макарычев ФГОС Задание 915

 

\[\boxed{\text{915\ (915).\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

Знаки сравнения:

\(> \ - \ \)больше;

\(\mathbf{<} -\) меньше.

При решении используем следующее:

1. Формулу умножения многочлена на многочлен – каждое число из первой скобки умножить на каждое число из второй:

\[\left( \mathbf{a + b} \right)\left( \mathbf{c + d} \right)\mathbf{= ac + ad + bc + bd.}\]

2. Если в неравенстве перенести слагаемое из одной части в другую, изменив его знак на противоположный, то получится неравенство, равносильное данному.

Решение.

\[\textbf{а)}\ (6y - 1)(y + 2) <\]

\[< (3y + 4)(2y + 1)\]

\[6y^{2} + 12y - y - 2 <\]

\[< 6y^{2} + 3y + 8y + 4\]

\[11y - 11y < 4 + 2\]

\[0 < 6 \Longrightarrow верно\ при\ любом\ y:\ \]

\[\ ч.т.д.\]

\[\textbf{б)}\ (3y - 1)(2y + 1) >\]

\[> (2y - 1)(2 + 3y)\]

\[6y^{2} + 3y - 2y - 1 >\]

\[> 4y + 6y^{2} - 2 - 3y\]

\[y - y > - 2 + 1\]

\[0 > - 1 \Longrightarrow верно\ при\ любом\ \]

\[\ y \Longrightarrow ч.т.д.\]

\[\boxed{\text{915.\ }\text{еуроки}\text{-}\text{ответы}\text{\ }\text{на}\text{\ }\text{пятёрку}}\]

\[\textbf{а)} - 1,5 \leq x \leq 4\]

\[\textbf{б)} - 2 < x < 1,3\]

\[\textbf{в)} - 5 \leq x \leq - 3\frac{1}{3}\]

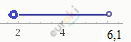
\[\textbf{г)}\ 2 < x < 6,1\]