Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по алгебре 8 класс Макарычев ФГОС Задание 856
Задание 856
\[\boxed{\text{856\ (856).\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
Пояснение.
| Неравенство, задающее числовой промежуток. | Обозначение и название числового промежутка. | Изображение числового промежутка на координатной прямой. |
|---|---|---|
| \[\mathbf{a \leq x \leq b}\] |
\[\left\lbrack \mathbf{a;\ b} \right\rbrack\mathbf{-}\] \[числовой\ отрезок\ \] |
 |
| \[\mathbf{a < x < b}\] |
\[\left( \mathbf{a;\ b} \right)\mathbf{- \ }\] \[\mathbf{интервал}\] |
 |
| \[\mathbf{a \leq x < b}\] |
\[\left\lbrack \mathbf{a;\ b} \right)\mathbf{-}\] \[\mathbf{полуинтервал}\] |
 |
| \[\mathbf{a < x \leq b}\] |
\[\left( \mathbf{a;\ b} \right\rbrack\mathbf{-}\] \[\mathbf{полуинтервал}\] |
 |
| \[\mathbf{x \geq a}\] |
\[\left\lbrack \mathbf{a; + \infty} \right)\mathbf{-}\] \[\mathbf{числовой\ луч}\] |
 |
| \[\mathbf{x > a}\] |
\[\mathbf{(a; + \infty) -}\] \[\mathbf{открытый\ числовой\ }\] \[\mathbf{луч}\] |
 |
| \[\mathbf{x \leq b}\] |
\[\left( \mathbf{- \infty;\ b} \right\rbrack\mathbf{-}\] \[\mathbf{числовой\ луч}\] |
 |
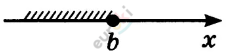| \[\mathbf{x < b}\] |
\[\left( \mathbf{- \infty;\ b} \right)\mathbf{-}\] \[\mathbf{открытый\ числовой\ }\] \[\mathbf{луч}\] |
 |
При решении используем следующее:
1. Чтобы сложить (вычесть) дроби с разными знаменателями, надо привести их к наименьшему общему знаменателю, затем сложить (вычесть) числители дробей, а знаменатель оставить без изменений.
2. Чтобы привести дроби к наименьшему общему знаменателю используем правило:
1. Найти наименьший общий знаменатель, который делится на каждый из знаменателей без остатка.
2. Найти дополнительный множитель, для каждого числителя, разделив общий знаменатель на знаменатели данных дробей.
3. Умножить числитель каждой дроби на дополнительный множитель.
3. Распределительное свойство умножения – число, стоящее перед скобкой, нужно умножить на каждое число в скобке:
\[\mathbf{a}\left( \mathbf{b - c} \right)\mathbf{= ab - ac.}\]
4. Если в неравенстве перенести слагаемое из одной части в другую, изменив его знак на противоположный, то получится неравенство, равносильное данному.
5. Если обе части неравенства умножить или разделить на одно и то же положительное число, то получится верное неравенство.
Решение.
\[\textbf{а)}\ \frac{2a - 1}{4} + \frac{a - 1}{3} > 0\]
\[6a - 3 + 4a - 4 > 0\]
\[10a > 7\]
\[a > 0,7\]
\[a \in (0,7;\ + \infty)\]
\[\textbf{б)}\ \frac{3b - 1}{2} - \frac{1 + 5b}{4} < 0\]
\[6b - 2 - 1 - 5b < 0\]
\[b < 3\]
\[b \in ( - \infty;3)\]
\[\boxed{\text{856.\ }\text{еуроки}\text{-}\text{ответы}\text{\ }\text{на}\text{\ }\text{пятёрку}}\]
\[Пусть\ x - путь\ Миши,\ тогда\]
\[\ \frac{S}{5}\ (ч) - время\ на\ весь\ путь.\]
\[Так\ как\ Коля\ 1\ часть\ пути\]
\[\ \left( \frac{S}{2} \right)\ \ шел\ со\ скоростью\]
\[\ V = 5 + 0,5 = 5,5\ \frac{км}{ч}.\]
\[t_{к1} = \frac{S}{2}\ :5,5 = \frac{S}{11}\ (ч),\]
\[а\ 2\ часть\ со\ скоростью:\]
\[V = 5 - 0,5 = 4,5\ \frac{км}{ч}.\]
\[t_{k2} = \frac{S}{2}\ :4,5 = \frac{S}{9}\ (ч).\]
\[\Longrightarrow \frac{S}{11} + \frac{S}{9} > \frac{S}{5} \Longrightarrow Коля\ прошел\ \]
\[быстрее\ и\ пришел\ первым.\]
\[Ответ:Коля.\]
