Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по алгебре 8 класс Макарычев ФГОС Задание 411
Задание 411
\[\boxed{\text{411\ (}\text{с}\text{).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
\[Выраж\mathbf{ение\ }\sqrt{\mathbf{x}}\mathbf{\ }\mathbf{имеет\ смысл}\]
\[\mathbf{при\ }\mathbf{x \geq 0}.\]
Решение.
\[\left( 2\sqrt{17} \right)^{2} > (4)^{2}\text{\ \ }\]
\[4 \cdot 17 > 16\ \]
\[68 > 16.\]
\[Что\ и\ требовалось\ доказать.\]
\[\left( 2\sqrt{2} \right)^{2} > \left( \sqrt{7} \right)^{2}\text{\ \ \ \ \ \ }\]
\[\ 4 \cdot 2 > 7\ \]
\[8 > 7.\]
\[Что\ и\ требовалось\ доказать.\]
\[\left( 6\sqrt{3} \right)^{2} > \left( 7\sqrt{2} \right)^{2}\]
\[36 \cdot 3 > 49\]
\[108 > 98.\]
\[Что\ и\ требовалось\ доказать.\]
\[\left( 8\sqrt{3} \right) < (14)^{2}\]
\[64 \cdot 3 < 196\]
\[192 < 196.\]
\[Что\ и\ требовалось\ доказать.\]
\[Ответ:выражение\ \sqrt{8\sqrt{3} - 14}\ \]
\[не\ имеет\ смысла.\ \]
\[\boxed{\text{411\ (}\text{н}\text{).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
\[\left( 2\sqrt{17} \right)^{2} > (4)^{2}\text{\ \ }\]
\[4 \cdot 17 > 16\ \ \]
\[68 > 16.\]
\[Ответ:утверждение\ неверно.\]
\[\textbf{б)}\ \sqrt{7\sqrt{2} - 6\sqrt{3}}\text{\ \ }не\ имеет\ \]
\[смысла,\ так\ как\ 7\sqrt{2} - 6\sqrt{3} < 0.\]
\[\left( 7\sqrt{2} \right)^{2} < \ \left( 6\sqrt{3} \right)^{2}\]
\[49 \cdot 2 < \ 36 \cdot 3\]
\[98 < 108\]
\[Ответ:утверждение\ верно.\]
\[\left( 8\sqrt{3} \right) < (14)^{2}\ \]
\[64 \cdot 3 < 196\ \ \]
\[192 < 196\]
\[Ответ:утверждение\ верно.\]
\[\left( 2\sqrt{2} \right)^{2} > \left( \sqrt{7} \right)^{2}\text{\ \ \ \ \ \ }\]
\[4 \cdot 2 > 7\ \ \]
\[8 > 7\]
\[Ответ:утверждение\ неверно.\]
\[\boxed{\text{411.}\text{\ }\text{еуроки}\text{-}\text{ответы}\text{\ }\text{на}\text{\ }\text{пятёрку}}\]
\[Формула\ Герона\ для\ \]
\[вычисления\ площади\ \]
\[треугольника:\]
\[S = \sqrt{p(p - a)(p - b)(p - c)};\ \ \]
\[p - полупериметр\ \]
\[треугольника.\]
Решение.
\[\textbf{а)}\ 12\ см,\ 16\ см,\ 24\ см:\]
\[p = \frac{12 + 16 + 24}{2} = 26\ (см).\]
\[= \sqrt{26 \cdot 14 \cdot 10 \cdot 2} =\]
\[= \sqrt{13 \cdot 2 \cdot 7 \cdot 2 \cdot 5 \cdot 2 \cdot 2} =\]
\[= 2 \cdot 2\sqrt{13 \cdot 7 \cdot 2} = 4\sqrt{455} =\]
\[= 4 \cdot 21 = 84\ см^{2}\text{.\ }\]
\[\textbf{б)}\ 18\ см,\ 22\ см,\ 26\ см:\]
\[p = \frac{18 + 22 + 26}{2} = \frac{66}{2} =\]
\[= 33\ (см).\]
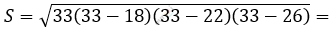
\[= \sqrt{33 \cdot 15 \cdot 11 \cdot 7} =\]
\[\sqrt{3 \cdot 11 \cdot 5 \cdot 3 \cdot 11 \cdot 7} =\]
\[= 11 \cdot 3\sqrt{5 \cdot 7} = 33\sqrt{35} \approx\]
\[\approx 33 \cdot 6 \approx 198\ \left( см^{2} \right).\]
\[\textbf{в)}\ a_{1} = 2a,\ \ b_{1} = 2b,\ \ \]
\[c_{1} = 2c:\]
\[p = \frac{2a + 2b + 2c}{2} =\]
\[= \frac{2(a + b + c)}{2} = 2p.\]
\[S_{1} = \sqrt{2p(2p - 2)(2p - 2)(2p - 2)} =\]
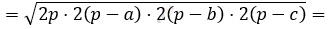
\[4\sqrt{p(p - a)(p - b)(p - c)} = 4S.\]
\[Ответ:увеличится\ в\ 4\ раза.\]
