Решебник по алгебре 8 класс Макарычев ФГОС Задание 396

 

\[\boxed{\text{396\ (396).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[\textbf{а)}\ \sqrt{a^{2}} = |a| = a;при\ \ a > 0\]

\[\textbf{б)}\ \sqrt{n^{2}} = |n| = - n;при\ \ n < 0\]

\[\textbf{в)}\ 3\sqrt{c^{2}} = 3 \cdot |c| = 3c;\ \]

\[при\ \ c > 0\]

\[3\sqrt{c^{2}} = 3 \cdot |0| = 0;при\ \ \ \ \ c = 0\]

\[\textbf{г)} - 5\sqrt{y^{2}} = - 5 \cdot |y| = - 5y;\ \]

\[при\ \ y > 0\]

\[\textbf{д)}\ \sqrt{36x^{2}} = 6 \cdot |x| = 6 \cdot ( - x) =\]

\[= - 6x;\ при\ \ x < 0\]

\[\sqrt{36x^{2}} = 0;при\ \ \ \ x = 0\]

\[\textbf{е)} - \sqrt{9y^{2}} = - 3 \cdot |y| =\]

\[= - 3 \cdot ( - y) = 3y;\ при\ \ y < 0\]

\[\textbf{ж)} - 5 \cdot \sqrt{4x^{2}} = - 5 \cdot 2 \cdot |x| =\]

\[= - 10x;\ при\ \ x > 0\]

\[- 5\sqrt{4x^{2}} = 0;\ при\ \ \ \ \ \ \ x = 0\]

\[\textbf{з)}\ 0,5 \cdot \sqrt{16a^{2}} = 0,5 \cdot 4 \cdot |a| =\]

\[= 2 \cdot ( - a) = - 2a;при\ \ a < 0\]

\[\boxed{\text{396.}\text{\ }\text{еуроки}\text{-}\text{ответы}\text{\ }\text{на}\text{\ }\text{пятёрку}}\]

Пояснение.

При любом значении x верно равенство:

\[\sqrt{\mathbf{x}^{\mathbf{2}}}\mathbf{=}\left| \mathbf{x} \right|\mathbf{.}\]

Модулем числа a называется само число a, если a>=0, или (-a), если a<0:

\[|a| = a;при\ a \geq 0;\]

\[|a| = - a;при\ a < 0.\]

Модуль числа всегда или положительное число, или равен 0.

Свойство степеней:

\[\mathbf{a}^{\mathbf{\text{mn}}}\mathbf{=}\left( \mathbf{a}^{\mathbf{m}} \right)^{\mathbf{n}}\mathbf{.}\]

Решение.

\[\mathbf{Представим\ подкоренные\ }\]

\[\mathbf{выражения\ в\ виде\ }\]

\[\mathbf{произведения\ простых\ }\]

\[\mathbf{множителей.}\]

\[\textbf{а)}\ \sqrt{20736} =\]

\[= \sqrt{2^{8} \cdot 3^{4}} = 2^{4} \cdot 3^{2} = 16 \cdot 9 =\]

\[= 144\]

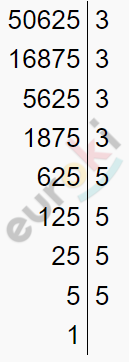
\[\textbf{б)}\ \sqrt{50625} =\]

\[= \sqrt{3 \cdot 3 \cdot 3 \cdot 3 \cdot 5 \cdot 5 \cdot 5 \cdot 5} =\]

\[= \sqrt{3^{4} \cdot 5^{4}} = 3^{2} \cdot 5^{2} = 9 \cdot 25 =\]

\[= 225\]

\[\textbf{в)}\ \sqrt{28224} =\]

\[= \sqrt{2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 3 \cdot 3 \cdot 7 \cdot 7} =\]

\[= \sqrt{2^{6} \cdot 3^{2} \cdot 7^{2}} = 2^{3} \cdot 3 \cdot 7 =\]

\[= 8 \cdot 21 = 168\]

\[\textbf{г)}\ \sqrt{680625} =\]

\[= \sqrt{3 \cdot 3 \cdot 5 \cdot 5 \cdot 5 \cdot 5 \cdot 11 \cdot 11} =\]

\[= \sqrt{3^{2} \cdot 5^{4} \cdot 11^{2}} =\]

\[= 3 \cdot 11 \cdot 5^{2} = 75 \cdot 11 = 825\ \]