Решебник по алгебре 8 класс Макарычев ФГОС Задание 242

 

\[\boxed{\text{242\ (242).\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\(= \frac{- x - 2}{2} = \frac{- x}{2} + 1\)

\[Отрицательно\ при\ x > 2\text{.\ }\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\text{242.\ }\text{еуроки}\text{-}\text{ответы}\text{\ }\text{на}\text{\ }\text{пятёрку}}\]

Пояснение.

Преобразуем правую часть равенства: приведем к общему знаменателю.

Затем приравняем числители (так как знаменатели равны).

Сгруппируем правую часть, составим систему уравнений и решим ее способом сложения.

Решение.

\[\textbf{а)}\ \frac{5x}{(x - 2)(x + 3)} =\]

\[= \frac{a^{\backslash x + 3}}{x - 2} + \frac{b^{\backslash x - 2}}{x + 3}\]

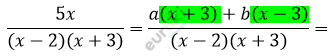
\[\frac{5x}{(x - 2)(x + 3)} =\]

\[= \frac{ax + 3a + bx - 2b}{(x - 2)(x + 3)}\]

\[5x = ax + bx + 3a - 2b\]

\[5x + 0 = x(a + b) + (3a - 2b)\]

\[\left\{ \begin{matrix} a + b = 5\ \ \ \ \\ 3a - 2b = 0 \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} a = 5 - b\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ 3(5 - b) - 2b = 0 \\ \end{matrix} \right.\ \]

\[15 - 3b - 2b = 0\]

\[15 - 5b = 0\]

\[b = 3\]

\[a = 5 - b = 5 - 3 = 2\]

\[Ответ:a = 2,\ b = 3.\]

\[\textbf{б)}\frac{5x + 31}{(x - 5)(x + 2)} =\]

\[= \frac{a^{\backslash x + 2}}{x - 5} - \frac{b^{\backslash x - 5}}{x + 2}\]

\[\frac{5x + 31}{(x - 5)(x + 2)} =\]

\[= \frac{ax + 2a - bx + 5b}{(x - 5)(x + 2)}\]

\[5x + 31 = x(a - b) + (2a + 5b)\]

\[\left\{ \begin{matrix} a - b = 5\ \ \ \ \ \ \ \ \\ 2a + 5b = 31 \\ \end{matrix} \right.\ \ \]

\[a = 5 + b\]

\[2(5 + b) + 5b = 31\]

\[10 + 2b + 5b = 31\]

\[7b = 21\]

\[b = 3\]

\[a = 5 + b = 5 + 3 = 8\]

\[Ответ:a = 8,\ b = 3.\]