Решебник по алгебре 8 класс Макарычев ФГОС Задание 170

\[\boxed{\text{170\ (170).\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[\textbf{б)}\ \frac{3}{\frac{1^{\backslash 4}}{2} + \frac{1^{\backslash 2}}{4} + \frac{1}{8}} = \frac{3}{\frac{4 + 2 + 1}{8}} =\]

\[= \frac{3 \cdot 8}{7} = \frac{24}{7} = 3\frac{3}{7}\]

\[\boxed{\text{170.\ }\text{еуроки}\text{-}\text{ответы}\text{\ }\text{на}\text{\ }\text{пятёрку}}\]

Пояснение.

Сначала сокращаем дробь. Приводим к общему знаменателю числитель и знаменатель, затем выполняем деление: умножаем числитель на дробь, обратную знаменателю.

Потом вместо букв подставляем данные значения.

Решение.

\[\textbf{а)}\ \frac{\frac{a^{2\ \backslash 9}}{4} - \frac{b^{2\ \backslash 4}}{9}}{\frac{a^{\backslash 3}}{12} + \frac{b^{\backslash 2}}{18}} =\]

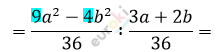
\[= \frac{(3a - 2b)(3a + 2b)}{36} \cdot \frac{36}{3a + 2b} =\]

\[= 3a - 2b\]

\[при\ a = \frac{2}{3};\ \ b = - \frac{1}{2}:\]

\[3 \cdot \frac{2}{3} - 2 \cdot \left( - \frac{1}{2} \right) = 2 + 1 = 3.\]

\[\textbf{б)}\ \ \frac{0,2a - b}{\frac{a^{2}}{25} - b^{2\ \backslash 25}} =\]

\[= \left( \frac{a}{5} - b^{\backslash 5} \right) \cdot \frac{25}{a^{2} - 25b^{2}} =\]

\[= \frac{a - 5b}{5} \cdot \frac{25}{(a - 5b)(a + 5b)} =\]

\[= \frac{5}{a + 5b}\]

\[при\ a = - 8;b = 0,6:\]

\[\frac{5}{- 8 + 5 \cdot 0,6} = \frac{5}{- 8 + 3} = \frac{5}{- 5} =\]

\[= - 1.\]