Решебник по алгебре 8 класс Макарычев ФГОС Задание 152

 

\[\boxed{\text{152\ (152).\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[\textbf{а)}\ \frac{a^{2} - 25}{a + 3} \cdot \frac{1}{a^{2} + 5a} - \frac{a + 5}{a^{2} - 3a} =\]

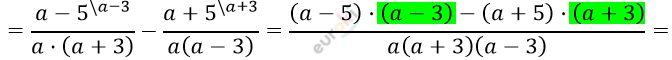
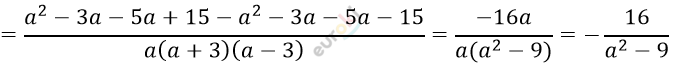
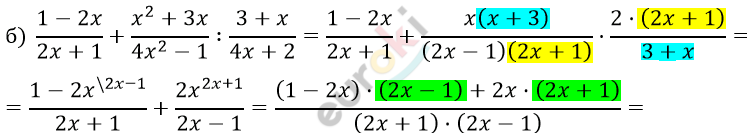
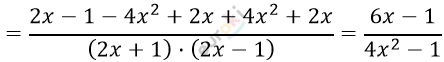
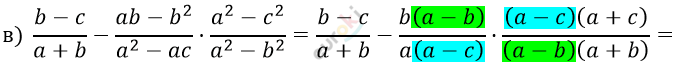
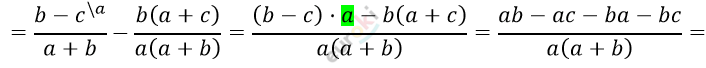
\[= \frac{- ac - bc}{a(a + b)} = \frac{- c \cdot (a + b)}{a(a + b)} =\]

\[= - \frac{c}{a}\]

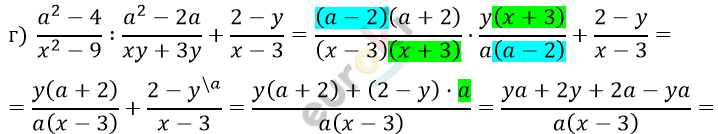
\[= \frac{2(y + a)}{a(x - 3)}\ \]

\[\boxed{\text{152.\ }\text{еуроки}\text{-}\text{ответы}\text{\ }\text{на}\text{\ }\text{пятёрку}}\]

Пояснение.

Порядок действий в сложных примерах:

• сначала выполняем действия в скобках;

• потом слева направо умножение и деление;

• затем слева направо сложение и вычитание.

Дроби с разным знаменателем приводим к общему знаменателю.

Чтобы разделить одну дробь на другую, нужно первую дробь умножить на дробь, обратную второй:

\[\frac{a}{b}\ :\frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c} = \frac{a \cdot d}{b \cdot c}.\]

Вспомним формулы сокращения:

\[a^{2} - b^{2} = (a - b)(a + b);\]

\[a^{2} + 2ab + b^{2} = (a + b)^{2};\]

\[a^{2} - 2ab + b^{2} = (a - b)^{2}.\]

Решение.

\[= \frac{5 \cdot 2 \cdot 4m}{4m(2m + 1)} = \frac{10}{2m + 1}\]

\[= \frac{x + 3}{x^{2} + 9} \cdot \frac{(x + 3)^{2} + (x - 3)^{2}}{(x + 3)(x - 3)} =\]

\[= \frac{x^{2} + 6x + 9 + x^{2} - 6x + 9}{\left( x^{2} + 9 \right)(x - 3)} =\]

\[= \frac{2x^{2} + 18}{\left( x^{2} + 9 \right)(x - 3)} =\]

\[= \frac{2\left( x^{2} + 9 \right)}{\left( x^{2} + 9 \right)(x - 3)} =\]

\[= \frac{2}{x - 3}\]