Решебник по алгебре 8 класс Макарычев ФГОС Задание 1144
Задание 1144



\[\boxed{\text{1144\ (1144).\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
Пояснение.
Модуль отрицательного числа – \(\mathbf{| -}\mathbf{a}\mathbf{| =}\mathbf{a}\);
Модуль положительного числа – \(\mathbf{|}\mathbf{a}\mathbf{| =}\mathbf{a}\).
Функция – это зависимость одной переменной величины (x) от другой (y).
Координаты точки – это пара чисел, в которой на первом месте стоит абсцисса (x), а на втором – ордината точки (у): A (x; y).
Координатная плоскость – две пересекающиеся под прямым углом прямые. В точке пересечения этих прямых находится начало координат (0;0). Горизонтальная прямая – ось x (справа откладываются положительные числа, слева отрицательные). Вертикальная прямая – ось y (сверху откладываются положительные числа, снизу отрицательные).
Алгоритм построения графика функции:
1. Подставим разные значения x в функцию, и для каждого x посчитаем значение y.
2. Ставим найденные координаты точек на координатной плоскости. Например, дана точка (4; -6). Четыре число положительное, поэтому двигаемся по оси x на 4 единицы вправо. Далее начинаем двигаться вниз по оси y на 6 единиц. Наносим точку.
3. После того, как нанесли все точки, соединяем их.
Решение.
\[\textbf{а)}\ y = |x + 2| + |x - 2|\]
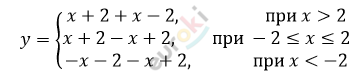
\[y = \left\{ \begin{matrix} 2x,\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ при\ x > 2 \\ 4,\ \ при\ - 2 \leq x \leq 2 \\ - 2x,\ \ \ \ \ \ \ \ \ \ \ \ \ при\ x < - 2 \\ \end{matrix} \right.\ \]
| \[x\] | \[3\] | \[4\] |
|---|---|---|
| \[y\] | \[6\] | \[8\] |
| \[x\] | \[- 2\] | \[2\] | \[0\] |
|---|---|---|---|
| \[y\] | \[4\] | \[4\] | \[4\] |
| \[x\] | \[- 3\] | \[- 4\] |
|---|---|---|
| \[y\] | \[6\] | \[8\] |

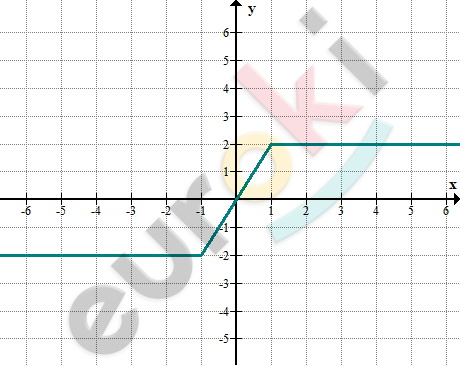
\[\textbf{б)}\ y = |x + 1| - |x - 1|\]

\[y = \left\{ \begin{matrix} 2,\ \ при\ x > 1\ \ \ \ \ \ \ \ \ \ \ (1) \\ 2x,\ при - 1 \leq x \leq x1\ \ (2) \\ - 2,\ \ \ \ \ \ \ \ \ при\ x < - 1\ \ \ \ \ (3) \\ \end{matrix} \right.\ \]
\[1)\ \]
| \[x\] | \[2\] | \[3\] | \[4\] |
|---|---|---|---|
| \[y\] | \[2\] | \[2\] | \[2\] |
\[2)\]
| \[x\] | \[- 1\] | \[0\] | \[1\] |
|---|---|---|---|
| \[y\] | \[- 2\] | \[0\] | \[2\] |
\[3)\]
| \[x\] | \[- 2\] | \[- 3\] |
|---|---|---|
| \[y\] | \[- 2\] | \[- 2\] |

\[\boxed{\text{1144.\ }\text{еуроки}\text{-}\text{ответы}\text{\ }\text{на}\text{\ }\text{пятёрку}}\]
\[\textbf{а)}\ y = \frac{1}{6x} + \frac{1}{6 + x}\]
\[\left\{ \begin{matrix} 6x \neq 0\ \ \ \ \ \ \\ 6 + x \neq 0\ \\ \end{matrix} \right.\ \Longrightarrow \left\{ \begin{matrix} x \neq 0\ \ \ \ \ \\ x \neq - 6\ \\ \end{matrix} \right.\ \]
\[D(y) =\]
\[= ( - \infty; - 6) \cup ( - 6;0) \cup (0; + \infty).\]
\[\textbf{б)}\ y = \sqrt{x} - \sqrt{x - 4}\]
\[\left\{ \begin{matrix} x \geq 0\ \ \ \ \ \ \ \\ x - 4 \geq 0 \\ \end{matrix} \right.\ \Longrightarrow \left\{ \begin{matrix} x \geq 0 \\ x \geq 4 \\ \end{matrix} \right.\ \Longrightarrow x \geq 4\]
\[D(y) = \lbrack 4; + \infty).\]
\[\textbf{в)}\ y = \frac{1}{1 + \frac{1}{x}}\ \]
\[\left\{ \begin{matrix} 1 + \frac{1}{x} \neq 0\ \\ x \neq 0\ \ \ \ \ \ \ \\ \end{matrix} \right.\ \Longrightarrow \left\{ \begin{matrix} \frac{1}{x} \neq - 1 \\ x \neq 0\ \ \ \ \\ \end{matrix} \right.\ \Longrightarrow\]
\[\Longrightarrow \left\{ \begin{matrix} x \neq - 1 \\ x \neq 0\ \ \ \\ \end{matrix} \right.\ \]
\[D(y) = ( - \infty; - 1) \cup ( - 1;0) \cup (0; + \infty).\]




