Решебник по алгебре 8 класс Макарычев ФГОС Задание 1128

 

\[\boxed{\text{1128\ (1128).\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

Иррациональные числа – это числа, которые нельзя записать обыкновенной дробью. Иррациональные числа – только бесконечные непериодические дроби (например: 1,3454466...., 3,45463....).

Свойства уравнений:

1. Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному;

2. Если обе части уравнения умножить или разделить на одно и то же число, отличное от нуля, то получится уравнение, равносильное данному.

Уравнения вида \(\mathbf{a}\mathbf{x}^{\mathbf{2}}\mathbf{+ bx + c = 0}\), где a, b и c – любые числа и a ≠ 0, называется квадратным уравнением.

Дискриминант – это формула, благодаря которой можно найти корни заданного квадратного уравнения:

\[\mathbf{D =}\mathbf{b}^{\mathbf{2}}\mathbf{- 4}\mathbf{\text{ac.}}\]

При решении используем следующее:

1. Если \(\mathbf{D > 0}\), то уравнение имеет 2 корня.

2. Если \(\mathbf{D = 0}\), то уравнение имеет 1 корень.

3. Если \(\mathbf{D < 0}\), то уравнение не имеет корней.

Решение.

\[x + \frac{1}{x} = n,\ \ n > 2\]

\[x^{2} - nx + 1 = 0,\ \ D = n^{2} - 4\]

\[1)\ n² - 4 < 0 - корней\ нет\]

\[2)\ n² - 4 = 0 - один\ корень:\]

\[n = 2.\]

\[3)\ n^{2} - 4 > 0 - два\ корня:\]

\[иррациональные\ оба.\]

\[\boxed{\text{1128.\ }\text{еуроки}\text{-}\text{ответы}\text{\ }\text{на}\text{\ }\text{пятёрку}}\]

\[y = \sqrt{x}.\]

\[\textbf{а)}\ y = 2\sqrt{x}\]

\[\textbf{б)}\ y = - \sqrt{x}\]

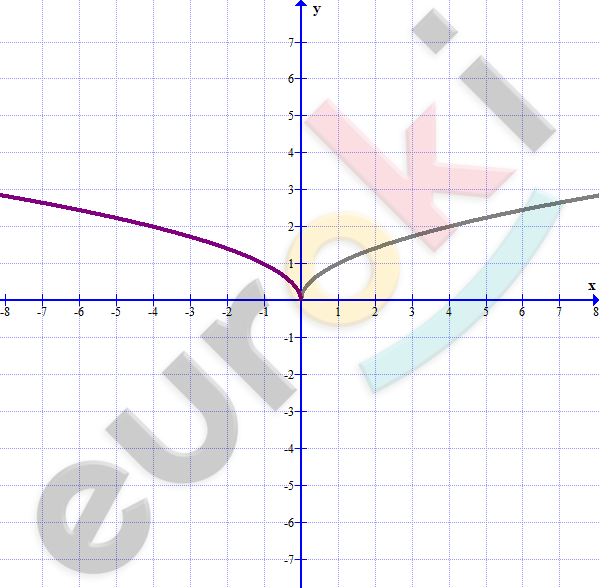
\[\textbf{в)}\ y = \sqrt{- x}\]