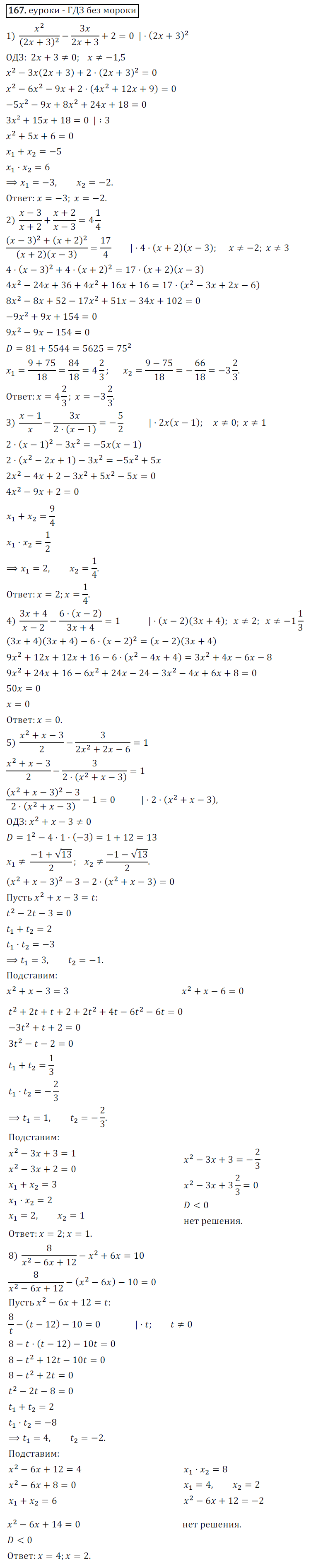Решебник по алгебре 8 класс Мерзляк дидактические материалы Вариант 1 | Номер 167

Условие:

Решите уравнение методом замены переменной:

1) x^2/(2x+3)^2-3x/(2x+3)+2=0;

2) (x-3)/(x+2)+(x+2)/(x-3)=41/4;

3) (x-1)/x-3x/2(x-1)=-5/2;

4) (3x+4)/(x-2)-6(x-2)/(3x+4)=1;

5) (x^2+x-3)/2-3/(2x^2+2x-6)=1;

6) (x^2-x-1)/x-6x/(x^2-x-1)=5;

7) 1/(x^2-3x+3)+2/(x^2-3x+4)=6/(x^2-3x+5);

8) 8/(x^2-6x+12)-x^2+6x=10.