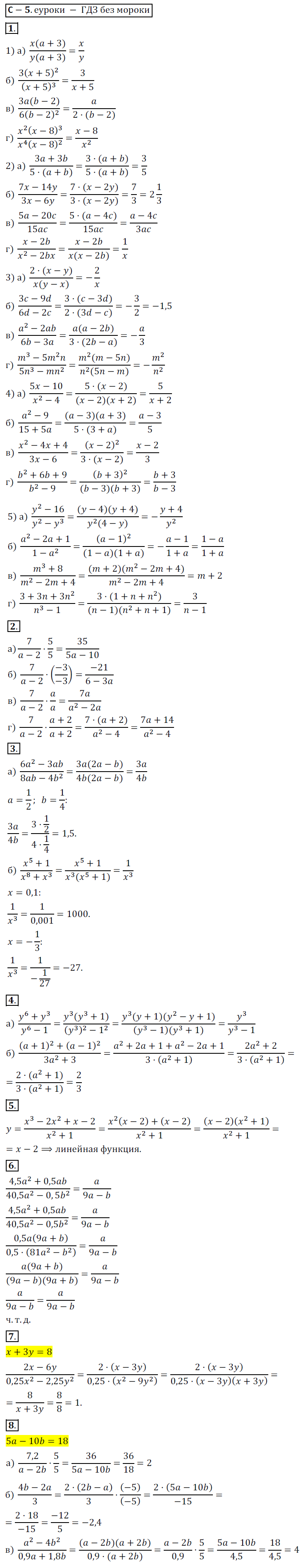ГДЗ по алгебре 8 класс Жохов дидактические материалы С-5(5). Сокращение дробей | Номер Вариант 1

Условие:

1. Сократите дробь:

1) а) (x(a+3))/(y(a+3));

б) (3(x+5)^2)/(x+5)^3;

в) (3a(b-2))/(6(b-2^2);

г) (x^2(x-8)^3)/(x^4(x-8)^2);

2) а) (3a+3b)/(5*(a+b));

б) (7x-14y)/(3x-6y);

в) (5a-20c)/15ac;

г) (x-2b)/(x^2-2bx);

3) а) (2(x-y))/(x(y-x));

б) (3c-9d)/(6d-2c);

в) (a^2-2ab)/(6b-3a);

г) (m^3-5m^2n)/(5n^3-mn^2);

4) а) (5x-10)/(x^2-4);

б) (a^2-9)/(15+5a);

в) (x^2-4x+4)/(3x-6);

г) (b^2+6b+9)/(b^2-9);

5) а) (y^2-16)/(4y^2-y^3);

б) (a^2-2a+1)/(1-a^2);

в) (m^3+8)/(m^2-2mn+4);

г) (3+3n+3n^2)/(n^3-1).

2. Приведите дробь 7/(a-2) к знаменателю:

а) 5a-10;

б) 6-3a;

в) a^2-2a;

г) a^2-4.

3. Найдите значение дроби:

а) (6a^2-3ab)/(8ab-4b^2) при a=1/2; b=1/4;

б) (x^5+1)/(x^8+3) при x=0,1; x=-1/3.

4. Сократите дробь:

а) (y^6+y^3)/(y^6-1);

б) ((a+1)^2+(a-1)^2)/(3a^2+3).

5. Докажите, что функция y=(x^3-2x^2+x-2)/(x^2+1) является линейной.

6. Докажите тождество (4,5a^2+0,5ab)/(40,5a^2-0,5b^2)=a/(9a-b).

7. Зная, что x+3y=8, найдите значение дроби (2x-6y)/(0,25x^2-2,25y^2).

8. Зная, что 5a-10b=18, найдите значение выражения:

а) 7,2/(a-2b);

б) (4b-2a)/3;

в) (a^2-4b^2)/(0,9a+1,8b).