Решебник по алгебре 7 класс Мерзляк ФГОС Задание 969

 

\[\boxed{\text{969\ (969).\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[ax + by = c\]

\[(3;5):\ \ \]

\[x + 5y = c,\ \ \]

\[3 + 5 \cdot 5 = 3 + 25 = 28\ \ \]

\[тогда:\]

\[x + 5y = 28.\]

\[\boxed{\text{969.\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[Пусть\ x\ км\ проятженность\ \]

\[Страстного\ бульвара,\ тогда\ \]

\[\frac{9}{11}x\ км - протяженность\ \]

\[Петровского\ бульвара,\ а\]

\[\frac{9}{11}x\ :2\frac{1}{7} = \frac{9}{11} \cdot \frac{7}{15}x =\]

\[= \frac{21}{55}\text{x\ }км - протяженность\ \]

\[Сретенского.\]

\[По\ условию\ задачи\ известно,\ \]

\[что\ общая\ протяженность\ \]

\[трех\ бульваров\ равна\ 1210\ м.\]

\[Составим\ уравнение:\]

\[x + \frac{9}{11}x + \frac{21}{55}x = 1210\ \ \ \ \ \ | \cdot 55\]

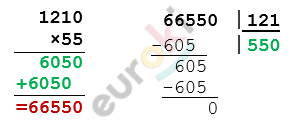
\[55x + 45x + 21x = 66\ 550\]

\[121x = 66\ 550\]

\[x = 66\ 550\ :121\]

\[x = 550\ (м) - протяженность\ \]

\[Страстного\ бульвара.\]

\[550 \cdot \frac{9}{11} = 50 \cdot 9 = 450\ (м) -\]

\[протяженность\ Петровского\ \]

\[бульвара.\]

\[550 \cdot \frac{21}{55} = 10 \cdot 21 = 210\ (м) -\]

\[протяженность\ Сретенского\ \]

\[бульвара.\ \]

\[Ответ:550\ м;\ \ 450\ м;\ \ 210\ м.\]