Решебник по алгебре 7 класс Мерзляк ФГОС Задание 718

 

\[\boxed{\text{718\ (718).\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[1)\ 15\text{cx} + 2\text{cy} - \text{cxy} - 30c =\]

\[= 15c(x - 2) - \text{cy}(x - 2) =\]

\[= (x - 2)\left( 15c - \text{cy} \right) =\]

\[= c \cdot (15 - y)(x - 2)\]

\[2)\ 35a² - 42ab + 10a^{2}b - 12ab^{2} =\]

\[= 5a^{2}(7 + 2b) - 6ab(7 + 2b) =\]

\[= (7 + 2b)\left( 5a^{2} - 6ab \right) =\]

\[= a \cdot (7 + 2b)(5a - 6b)\]

\[3)\ x^{3} + x^{2}y + x^{2} + xy =\]

\[= x^{2}(x + y) + x(x + y) =\]

\[= (x + y)\left( x^{2} + x \right) =\]

\[= x \cdot (x + y)(x + 1)\]

\[4)\ mn^{4} - n^{4} + mn^{3} - n^{3} =\]

\[= n^{4}(m - 1) + n^{3}(m - 1) =\]

\[= (m - 1)\left( n^{4} + n^{3} \right) =\]

\[= n^{3}(m - 1)(n + 1)\]

\[\boxed{\text{718.\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[Пусть\ даны\ последовательные\ \]

\[натуральные\ числа\ \]

\[(с\ меньшего):\ \ \ \]

\[n,\ \ \ n + 1,\ \ \ n + 2,\ \ \ n + 3.\]

\[(n + 1)^{2} + (n + 3)^{2} - сумма\ \]

\[квадратов\ второго\ и\ \]

\[четвертого\ чисел\ на\ 82\ \]

\[больше,\ чем\]

\[n^{2} + (n + 2)^{2} - сумма\ \]

\[квадратов\ первого\ и\ третьего\ \]

\[чисел.\]

\[Составим\ уравнение:\]

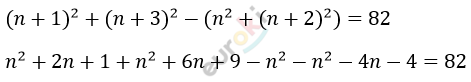
\[4n = 76\]

\[n = 19 - первое\ число.\]

\[19,\ 20,\ 21,\ 22 - искомые\ числа.\]

\[Ответ:19,\ 20,\ 21,\ 22.\]