Решебник по алгебре 7 класс Мерзляк ФГОС Задание 675

 

\[\boxed{\text{675\ (675).\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[a^{3} - 27 = a^{3} - 3^{3} =\]

\[= (a - 3)\left( a^{2} + 3a + 9 \right)\]

\[Ответ:4).\]

\[\boxed{\text{675.\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

Решение.

\[1)\ Пусть\ 2n\ и\ (2n + 2) - два\ \]

\[последовательных\ четных\ \]

\[числа.\]

\[Найдем\ разность\ их\ \]

\[квадратов:\ \]

\[(2n + 2)^{2} - (2n)^{2} =\]

\[= (2n + 2 - 2n)(2n + 2 + 2n) =\]

\[= 2 \cdot (4n + 2).\]

\[Найдем\ их\ удвоенную\ сумму:\]

\[2 \cdot (2n + 2 + 2n) = 2 \cdot (4n + 2).\]

\[Разность\ квадратов\ двух\ \]

\[последовательных\ четных\ \]

\[чисел\ равна\]

\[удвоенной\ сумме\ этих\ чисел:\]

\[2 \cdot (4n + 2) = 2 \cdot (4n + 2).\]

\[Что\ и\ требовалось\ доказать.\]

\[2)\ Пусть\ (2n - 1)\ и\ (2n + 1) -\]

\[два\ последовательных\ \]

\[нечетных\ числа.\]

\[Найдем\ разность\ их\ квадратов:\]

\[(2n + 1)^{2} - (2n - 1)^{2} =\]

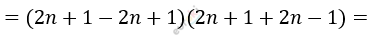
\[= 2 \cdot 4n = 8n \Longrightarrow делится\ на\ 8.\]

\[Что\ и\ требовалось\ доказать.\]