Решебник по алгебре 7 класс Мерзляк ФГОС Задание 498
Задание 498



\[\boxed{\text{498\ (498).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
\[В\ каждом\ матче\ участвует\ 2\ \]
\[теннисиста\ и\ один\ из\ них\ \]
\[выбывает.\ Так\ как\ после\ \]
\[каждого\ матча\ выбывает\ один\ \]
\[теннисист,\ то\ необходимо\ \text{n~}\]
\[матчей,\ чтобы\ выбыли\ все\ \]
\[теннисисты.\ Но\ так\ как\ в\ \]
\[турнире\ выбывают\ не\ все\ \]
\[теннисисты,\ а\ остается\ один\ \]
\[победитель,\ то\ необходимо\ \]
\[провести\text{~\ }(n\ - \ 1)\ матч\ для\ \]
\[определения\ этого\ \]
\[победителя.\]
\[Ответ:(n - 1)\ матч.\ \]

\[\boxed{\text{498.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
Пояснение.

Решение.
\[1)\ (a - 2) \cdot (b + 5) =\]
\[= ab + 5a - 2b - 10.\]
\[2)\ (m + n) \cdot (p - k) =\]
\[= mp - km + np - kn.\]
\[3)\ (x - 8) \cdot (x + 4) =\]
\[= x^{2} + 4x - 8x - 32 =\]
\[= x^{2} - 4x - 32.\]
\[4)\ (x - 10) \cdot (x - 9) =\]
\[= x^{2} - 9x - 10x + 90 =\]
\[= x^{2} - 19x + 90.\]
\[5)\ (c + 5) \cdot (c + 8) =\]
\[= c^{2} + 8c + 5c + 40 =\]
\[= c^{2} + 13c + 40.\]
\[6)\ (3y + 1) \cdot (4y - 6) =\]
\[= 12y^{2} - 18y + 4y - 6 =\]
\[= 12y^{2} - 14y - 6.\]
\[7)\ ( - 2m - 3) \cdot (5 - m) =\]
\[= - 10m + 2m^{2} - 15 + 3m =\]
\[= 2m^{2} - 7m - 15.\]
\[8)\ \left( 5x^{2} - x \right) \cdot \left( 6x^{2} + 4x \right) =\]
\[= 30x^{4} + 20x^{3} - 6x^{3} - 4x^{2} =\]
\[= 30x^{4} + 14x^{3} - 4x^{2}.\]
\[9)\ ( - c - 4) \cdot \left( c^{3} + 3 \right) =\]
\[= - c^{4} - 4c^{3} - 3с - 12.\]
\[10)\ (x - 5) \cdot \left( x^{2} + 4x - 3 \right) =\]
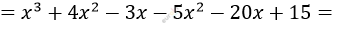
\[= x^{3} - x^{2} - 23x + 15.\]
\[11)\ (2a + 3) \cdot \left( 4a^{2} - 4a + 3 \right) =\]
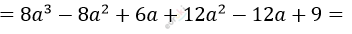
\[= 8a^{3} + 4a^{2} - 6a + 9.\]
\[12)\ a \cdot (5a - 4) \cdot (3a - 2) =\]
\[= \left( 5a^{2} - 4a \right) \cdot (3a - 2) =\]
\[= 15a^{3} - 10a^{2} - 12a^{2} + 8a =\]
\[= 15a^{3} - 22a^{2} + 8a.\ \]





