Решебник по алгебре 7 класс Мерзляк ФГОС Задание 39
Задание 39



\[\boxed{\text{39\ (39).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
\[1)\ 0,8 - (1,5x - 2) =\]
\[= - 0,8 + 4,5x\]
\[0,8 - 1,5x + 2 = - 0,8 + 4,5x\]
\[- 1,5x - 4,5x = - 0,8 - 0,8 - 2\]
\[- 6x = - 3,6\]
\[x = 3,6\ :6\]
\[x = 0,6\]
\[Ответ:x = 0,6.\]
\[2)\ 0,6x - 5 \cdot (0,3x + 0,2) =\]
\[= 0,5 \cdot (x - 1) - 0,8\]
\[0,6x - 1,5x - 1 =\]
\[= 0,5x - 0,5 - 0,8\]
\[- 0,9x - 0,5x = 1 - 1,3\]
\[- 1,4x = - 0,3\]
\[x = 0,3\ :1,4\]
\[x = \frac{3}{14}\]
\[Ответ:x = \frac{3}{14}.\]

\[\frac{7}{7 \cdot 8}y + \frac{7}{7} - \frac{3 \cdot 2}{4 \cdot 9}y - \frac{3 \cdot 16}{4 \cdot 9} =\]
\[= \frac{1}{12}\]
\[\frac{1^{\backslash 3}}{8}y + 1 - \frac{1^{\backslash 4}}{6}y - \frac{4}{3} = \frac{1}{12}\]
\[\frac{3}{24}y - \frac{4}{24}y = \frac{1}{12} - 1 + \frac{4}{3}\]
\[- \frac{1}{24}y = \frac{1}{12} + \frac{1^{\backslash 4}}{3}\]
\[- \frac{1}{24y} = \frac{1}{12} + \frac{4}{12}\]
\[- \frac{1}{24}y = \frac{5}{12}\]
\[y = \frac{5}{12}\ :\left( - \frac{1}{24} \right)\]
\[y = - \frac{5 \cdot 24}{12} = - 5 \cdot 2\]
\[y = - 10\]
\[Ответ:\ y = - 10.\]
\[4)\ \frac{5}{27} \cdot (5,4 - 8,1y) =\]
\[= 0,03 + \frac{4}{17} \cdot (6,8 - 3,4y)\]
\[\frac{5}{27} \cdot \left( \frac{54}{10} - \frac{81}{10}y \right) =\]
\[= 0,03 + \frac{4}{17} \cdot \left( \frac{68}{10} - \frac{34}{10}y \right)\]
\[\frac{5 \cdot 54}{27 \cdot 10} - \frac{5 \cdot 81}{27 \cdot 10}y =\]
\[= \frac{3}{100} + \frac{4 \cdot 68}{17 \cdot 10} - \frac{4 \cdot 34}{17 \cdot 10}y\]
\[1 - \frac{3}{2}y = \frac{3}{100} + \frac{8}{5} - \frac{4}{5}y\]
\[- 1,5y + 0,8y = 0,03 + 1,6 - 1\]
\[- 0,7y = 0,63\]
\[y = 0,63\ :( - 0,7)\]
\[y = - 0,9\]
\[Ответ:\ y = - 0,9.\]

\[\boxed{\text{39.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
\[1)\ 288\]
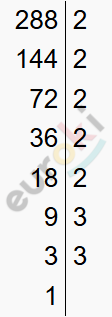
\[2)\ 693\]






