Решебник по алгебре 7 класс Макарычев ФГОС Задание 98

 

\[\boxed{\text{98.}\text{\ }еуроки - ответы\ на\ пятёрку}\]

Пояснение.

В любом произведении можно как угодно (как удобно) переставлять множители и любым образом объединять их в группы.

Распределительное свойство:

\[ab + ac = a(b + c);\]

\[ab - ac = a(b - c).\]

Решение.

\[\textbf{а)}\ 24 \cdot 17 + 17 \cdot 6 =\]

\[= 17 \cdot (24 + 6) = 17 \cdot 30 =\]

\[\Longrightarrow так\ как\ среди\ множителей\ \]

\[есть\ число\ 5 \Longrightarrow\]

\[\Longrightarrow выражение\ (24 \cdot 17 + 17 \cdot 6)\ \]

\[делится\ на\ 5.\]

\[\textbf{б)}\ 34 \cdot 85 + 34 \cdot 36 =\]

\[= 34 \cdot (85 + 36) = 34 \cdot 121 =\]

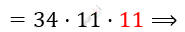
\[\Longrightarrow так\ как\ среди\ множителей\ \]

\[есть\ число\ 11 \Longrightarrow\]

\[\Longrightarrow выражение\ \ \]

\[(34 \cdot 85 + 34 \cdot 36)\ делится\ \]

\[на\ 11.\]

\[\boxed{\text{98\ (98).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

Решение.

\[\textbf{а)}\ x\mathbf{+}(b + c + d - m) =\]

\[= x + b + c + d - m\]

\[знаки\ слагаемых\ сохраняем.\]

\[\textbf{б)}\ a - (b - c - d) =\]

\[= a - b + c + d\]

\[знаки\ слагаемых\ меняем\ на\ \]

\[противоположные.\]

\[\textbf{в)}\ x + y - (b + c - m) =\]

\[= x + y - b - c + m\]

\[знаки\ слагаемых\ меняем\ на\ \]

\[противоположные.\]

\[\textbf{г)}\ x + (a - b) - (c + d) =\]

\[= x + a - b - c - d\]

\[в\ первой\ скобке\ знаки\ \]

\[сохраняем,\ во\ второй - меняем\ \]

\[на\ противоположные.\]