Решебник по алгебре 7 класс Макарычев ФГОС Задание 585

\[\boxed{\text{585.}\text{\ }еуроки - ответы\ на\ пятёрку}\]

Пояснение.

Подобными членами называются слагаемые многочлена, которые имеют одинаковую буквенную часть.

Чтобы сложить (привести) подобные слагаемые, надо сложить их коэффициенты и результат умножить на общую буквенную часть.

Чтобы привести многочлен к стандартному виду, нужно привести подобные члены.

Решение.

\[\mathbf{Приведем\ многочлен\ к\ }\]

\[\mathbf{стандартному\ виду\ и\ найдем\ }\]

\[\mathbf{значение,равное\ }\mathbf{3}\mathbf{a}^{\mathbf{2}}\mathbf{+ b.}\]

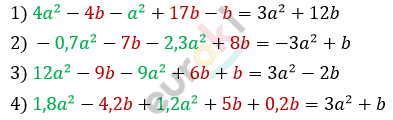
\[Ответ:многочлен\ 4).\]

\[\boxed{\text{585\ (585).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

Решение.

\[\textbf{а)}\ \left( 4x^{3} - 5x - 7 \right) + \left( x^{3} - 8x \right) =\]

\[= 5x^{3} - 13x - 7\]

\[\textbf{б)}\ \left( 5y^{2} - 9 \right) - \left( 7y^{2} - y + 5 \right) =\]

\[= - 2y^{2} + y - 14\ \]