Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по алгебре 7 класс Макарычев ФГОС Задание 320
Задание 320
\[\boxed{\text{320.}\text{\ }еуроки - ответы\ на\ пятёрку}\]
Пояснение.
График линейной функции задается формулой y=kx+b.
Чтобы узнать формулу графика на рисунке, нужно взять любую точку, подставить ее в формулу y=kx+b, найти значение k.
После подставить найденное значение в формулу и получить формулу графика.
Решение.
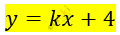
\[\textbf{а)}\ при\ k = - 1\ график\ функции\ \]
\[y = kx + 4\ параллелен\ графику\]
\[функции\ y = - x.\]
\[\textbf{б)}\ при\ k = 0\ график\ функции\ \]
\[y = kx + 4\ не\ пересекает\ ось\ x.\]
\[\textbf{в)}\ пересекает\ ось\ абцисс\ \]
\[в\ точке\ (3;0):\]
\[y = kx + 4\]
\[0 = 3k + 4\]
\[3k = - 4\]
\[k = - \frac{4}{3}\]
\[k = - 1\frac{1}{3}\text{.\ }\]
\[\textbf{г)}\ 12 - x = x + 4\]
\[2x = 8\]
\[x = 4;\]
\[y = 12 - 4 = 8;\]
\[точка\ (4;8) - точка\ \]
\[пересечения\ графиков\ \]
\[y = 12 - x\ \ \ и\ \ y = x + 4.\]
\[8 = 4k + 4\]
\[4k = 4\]
\[k = 1.\]
\[При\ k = 1\ график\ функции\ \]
\[y = kx + 4\ проходит\ через\ \]
\[точку\ пересечения\ графиков\ \]
\[функций\ y = 12 - x\ и\ \]
\[y = x + 4.\]
\[\boxed{\text{320\ (320).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
\[\textbf{а)}\ при\ k = - 1\ график\ функции\ \]
\[y = kx + 4\ параллелен\ графику\]
\[функции\ y = kx + 4.\]
\[\textbf{б)}\ при\ k = 0\ график\ функции\ \]
\[y = kx + 4\ не\ пересекает\ ось\ x.\]
\[\textbf{в)}\ пересекает\ ось\ абцисс\ \]
\[в\ точке\ (3;0):\]
\[y = kx + 4\]
\[0 = 3k + 4\]
\[3k = - 4\]
\[k = - \frac{4}{3}\]
\[k = - 1\frac{1}{3}\text{.\ }\]
\[\textbf{г)}\ 12 - x = x + 4\]
\[2x = 8\]
\[x = 4;\]
\[y = 12 - 4 = 8;\]
\[точка\ (4;8) - точка\ \]
\[пересечения\ графиков\ \]
\[y = 12 - x\ \ \ и\ \ y = x + 4.\]
\[8 = 4k + 4\]
\[4k = 4\]
\[k = 1.\]
\[При\ k = 1\ график\ функции\ \]
\[y = kx + 4\ проходит\ через\ \]
\[точку\ пересечения\ графиков\ \]
\[функций\ y = 12 - x\ и\ \]
\[y = x + 4.\]
