Решебник по алгебре 7 класс Макарычев ФГОС Задание 1167

 

\[\boxed{\text{1167.}\text{\ }еуроки - ответы\ на\ пятёрку}\]

\[\textbf{а)}\ 3 \cdot (x - 2y) -\]

\[- 2 \cdot (x - 4y) = 4\]

\[3x - 6y - 2x + 8y = 4\]

\[x + 2y = 4\]

\[y = 2 - 0,5x\]

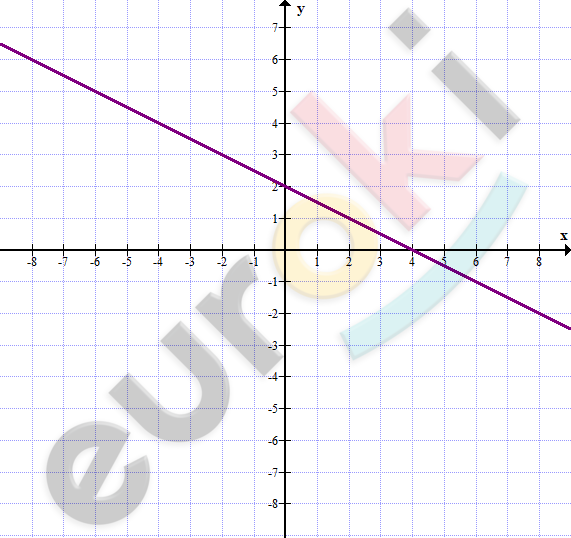
\[\textbf{б)}\ 2 \cdot (0,5x - 1,2y) -\]

\[- (0,6y + x) = 6\]

\[x - 2,4y - 0,6y - x = 6\]

\[- 3y = 6\]

\[y = - 2\]

\[\textbf{в)}\ 3 \cdot (0,4y - 0,2x) -\]

\[- 4 \cdot (0,3y - 0,6x) = 0,6\]

\[1,2y - 0,6x - 1,2y + 2,4x = 0,6\]

\[1,8x = 0,6\]

\[x = \frac{6}{18} = \frac{1}{3}\]

\[\boxed{\text{1167\ (1167).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

Системой линейных уравнений называют два и более уравнения с несколькими переменными (буквы x, y и т.д.), для которых необходимо найти общее решение.

Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство.

Линейным уравнением с двумя переменными называется уравнение вида

\(\mathbf{ax + by = c,}\) где x и y – переменные, a, b и с – некоторые числа.

Если\(\mathbf{\ }\mathbf{c}_{\mathbf{1}}\mathbf{\neq}\mathbf{c}_{\mathbf{2}}\), то графики параллельны и система не имеет решений.

Если обе части уравнения умножить или разделить на одно и то же число, отличное от нуля, то получится уравнение, равносильное данному.

Решение.

\[\left\{ \begin{matrix} \frac{1}{2}x + \frac{1}{5}y = 2\ \ | \cdot 10 \\ 5x + 2y = c\ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \Longrightarrow\]

\[\Longrightarrow \left\{ \begin{matrix} 5x + 2y = 20 \\ 5x + 2y = c\ \ \ \\ \end{matrix} \right.\ ,\ \ при\]

\[c \neq 20\ \ система\ не\ имеет\ \]

\[решений.\]

\[Ответ:при\ c \neq 20.\]