Решебник по алгебре 11 класс Никольский Параграф 8. Уравнения-следствия Задание 35

\[\boxed{\mathbf{35.}}\]

\[\textbf{а)}\ \sqrt{\frac{x - 1}{x - 2} + \sqrt{x}} = \sqrt{\frac{2x - 2}{x - 6} + \sqrt{x}}\]

\[x \geq 0;x \neq 2;x \neq 6.\]

\[\frac{x - 1}{x - 2} + \sqrt{x} = \frac{2x - 2}{x - 6} + \sqrt{x}\]

\[\frac{x - 1}{x - 2} - \frac{2x - 2}{x - 6} = 0\]

\[\frac{(x - 1)(x - 6) - (2x - 2)(x - 2)}{(x - 2)(x - 6)} = 0\]

\[x^{2} - x - 6x + 6 - 2x^{2} + 2x + 4x - 4 = 0\]

\[- x^{2} - x + 2 = 0\]

\[x^{2} + x - 2 = 0\]

\[x_{1} + x_{2} = - 1;\ \ x_{1} \cdot x_{2} = - 2\]

\[x_{1} = - 2;\ \ \ x_{2} = 1.\]

\[Ответ:x = 1.\]

\[\textbf{б)}\ \sqrt{\frac{x + 3}{x - 3} + \sqrt{x}} = \sqrt{\frac{2x - 6}{x - 4} + \sqrt{x}}\]

\[x > 0;\ \ x \neq 3;\ \ x \neq 4.\]

\[\frac{x + 3}{x - 3} + \sqrt{x} = \frac{2x - 6}{x - 4} + \sqrt{x}\]

\[\frac{x + 3}{x - 3} - \frac{2x - 6}{x - 4} = 0\]

\[- x^{2} + 11x - 30 = 0\]

\[x^{2} - 11x + 30 = 0\]

\[x_{1} + x_{2} = 11;\ \ \ x_{1} \cdot x_{2} = 30\]

\[x_{1} = 5;\ \ x_{2} = 6.\]

\[Ответ:x = 5;\ \ x = 6.\]

\[\textbf{в)}\ \sqrt{\frac{x + 1}{x - 3} + 3tg\frac{\text{πx}}{4}} =\]

\[= \sqrt{\frac{x + 4}{3x - 8} + 3tg\frac{\text{πx}}{4}}\]

\[x \neq 3;\ \ x \neq \frac{8}{3}.\]

\[\frac{x + 1}{x - 3} + 3tg\frac{\text{πx}}{4} = \frac{x + 4}{3x - 8} + 3tg\frac{\text{πx}}{4}\]

\[\frac{x + 1}{x - 3} - \frac{x + 4}{3x - 8} = 0\]

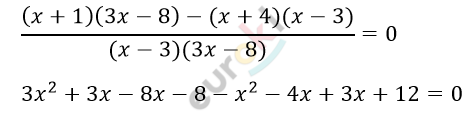
\[2x^{2} - 6x + 4 = 0\ \ |\ :2\]

\[x^{2} - 3x + 2 = 0\]

\[x_{1} + x_{2} = 3;\ \ x_{1} \cdot x_{2} = 2\]

\[x_{1} = 1;\ \ x_{2} = 2.\]

\[\text{tg}\frac{\text{πx}}{4} \neq \frac{\pi}{2}:\]

\[x \neq 2.\]

\[Ответ:x = 1.\]

\[\textbf{г)}\ \sqrt{\frac{x - 3}{x + 2} - tg\ \frac{\text{πx}}{4}} =\]

\[= \sqrt{\frac{x - 3}{2x + 3} - tg\ \frac{\text{πx}}{4}}\]

\[\text{tg}\frac{\text{πx}}{4} \neq \frac{\pi}{2}:\]

\[x \neq 2.\]

\[x \neq - 2;\ \ x \neq - 1,5.\]

\[\frac{x - 3}{x + 2} - tg\ \frac{\text{πx}}{4} = \frac{x - 3}{2x + 3} - tg\ \frac{\text{πx}}{4}\]

\[\frac{x - 3}{x + 2} - \frac{x - 3}{2x + 3} = 0\]

\[\frac{(x - 3)(2x + 3) - (x - 3)(x + 2)}{(x + 2)(2x + 3)} = 0\]

\[(x - 3)(2x + 3 - x - 2) = 0\]

\[(x - 3)(x + 1) = 0\]

\[x = 3;\ \ x = - 1.\]

\[Проверка.\]

\[x = - 1:\]

\[\sqrt{\frac{- 1 - 3}{- 1 + 2} - ( - 1)} =\]

\[= \sqrt{\frac{- 1 - 3}{- 2 + 3} - ( - 1)}\]

\[\sqrt{- 4 + 1} = \sqrt{- 4 + 1}\]

\[не\ имеет\ смысла.\]

\[Ответ:x = 3.\]