Решебник по алгебре 11 класс Никольский Параграф 6. Первообразная и интеграл Задание 9

\[\boxed{\mathbf{9}.}\]

\[\textbf{а)}\ f(x) = \frac{x^{- 3}\sqrt{x}}{x^{2}} = \frac{x^{- 3} \cdot x^{\frac{1}{2}}}{x^{2}} =\]

\[= x^{- 4,5};\]

\[\int_{}^{}{x^{- 4,5}\text{dx}} = \frac{x^{- 4,5 + 1}}{- 4,5 + 1} + C =\]

\[= \frac{x^{- 3,5}}{- 3,5} + C = - \frac{2}{7x^{3}\sqrt{x}} + C;\]

\[F(x) = - \frac{2}{7x^{3}\sqrt{x}} + C.\]

\[\textbf{б)}\ f(x) = \frac{x^{3}\sqrt{x^{- 5}}}{x^{- 2}} = \frac{x^{3} \cdot x^{- \frac{5}{2}}}{x^{- 2}} =\]

\[= x^{2,5};\]

\[\int_{}^{}{x^{2,5}\text{dx}} = \frac{x^{2,5 + 1}}{2,5 + 1} + C =\]

\[= \frac{x^{3,5}}{3,5} + C = \frac{2x^{3,5}}{7} + C =\]

\[= \frac{2}{7}x^{3}\sqrt{x} + C;\]

\[F(x) = \frac{2}{7}x^{3}\sqrt{x} + C.\]

\[\textbf{в)}\ f(x) = \frac{x\sqrt{x}}{\sqrt[3]{x}} = \frac{x \cdot x^{\frac{1}{2}}}{x^{\frac{1}{3}}} = x^{\frac{7}{6}};\]

\[\int_{}^{}{x^{\frac{7}{6}}\text{dx}} = \frac{x^{\frac{7}{6} + 1}}{\frac{7}{6} + 1} + C = \frac{x^{2\frac{1}{6}}}{2\frac{1}{6}} + C =\]

\[= \frac{6x^{\frac{13}{6}}}{13} + C = \frac{6}{13}x^{2} \cdot \sqrt[6]{x} + C;\]

\[F(x) = \frac{6}{13}x^{2} \cdot \sqrt[6]{x} + C.\]

\[\textbf{г)}\ f(x) = \frac{x \cdot \sqrt[3]{x^{2}}}{\sqrt{x}} = \frac{x \cdot x^{\frac{2}{3}}}{x^{\frac{1}{2}}} = x^{\frac{7}{6}};\]

\[\int_{}^{}{x^{\frac{7}{6}}\text{dx}} = \frac{x^{\frac{7}{6} + 1}}{\frac{7}{6} + 1} + C = \frac{x^{2\frac{1}{6}}}{2\frac{1}{6}} + C =\]

\[= \frac{6x^{\frac{13}{6}}}{13} + C = \frac{6}{13}x^{2} \cdot \sqrt[6]{x} + C;\]

\[F(x) = \frac{6}{13}x^{2} \cdot \sqrt[6]{x} + C.\]

\[\textbf{д)}\ f(x) = \sqrt[3]{(7x - 9)^{2}} =\]

\[= (7x - 9)^{\frac{2}{3}};\]

\[\frac{1}{7}\int_{}^{}{(7x - 9)^{\frac{2}{3}}d(7x - 9)} =\]

\[= \frac{1}{7} \cdot \frac{(7x - 9)^{\frac{2}{3} + 1}}{\frac{2}{3} + 1} + C =\]

\[= \frac{1}{7} \cdot \frac{(7x - 9)^{\frac{5}{3}}}{\frac{5}{3}} + C =\]

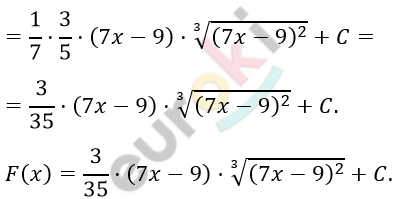
\[\textbf{е)}\ f(x) = \sqrt[4]{(5x + 1)^{3}} =\]

\[= (5x + 1)^{\frac{3}{4}};\]

\[\frac{1}{5}\int_{}^{}{(5x + 1)^{\frac{3}{4}}d(5x + 1)} =\]

\[= \frac{1}{5} \cdot \frac{(5x + 1)^{\frac{3}{4} + 1}}{\frac{3}{4} + 1} + C =\]

\[= \frac{1}{5} \cdot \frac{(5x + 1)^{\frac{7}{4}}}{\frac{7}{4}} + C =\]

\[F(x) =\]

\[= \frac{4}{35} \cdot (5x + 1) \cdot \sqrt[4]{(5x + 1)^{3}} + C.\]