Решебник по алгебре 11 класс Никольский Параграф 6. Первообразная и интеграл Задание 56

\[\boxed{\mathbf{56}.}\]

\[\textbf{а)}\ y = \sin x;\ \ \]

\[x = - \pi;x = \pi;y = 0;\]

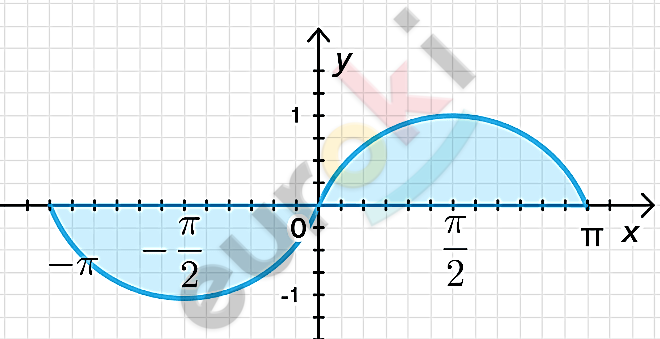
\[Фигура\ симметрична\ \]

\[относительно\ начала\ \]

\[координат,\ а\ площади\ \]

\[симметричных\ частей\ равны.\]

\[S = 2\int_{0}^{\pi}{\sin x\text{dx}} =\]

\[= \left. \ \left( - 2\cos x \right) \right|_{0}^{\pi} =\]

\[= - 2\cos\pi - \left( - 2\cos 0 \right) =\]

\[= 2 + 2 = 4\ кв.\ ед.\]

\[\textbf{б)}\ y = \sin x;\ \ \]

\[x = 0;x = 2\pi;y = 0;\]

\[Фигура\ симметрична\ \]

\[относительно\ x = \pi,\ а\ \]

\[площади\ симметричных\ \]

\[частей\ равны.\]

\[S = 2\int_{0}^{\pi}{\sin x\text{dx}} =\]

\[= \left. \ \left( - 2\cos x \right) \right|_{0}^{\pi} =\]

\[= - 2\cos\pi - \left( - 2\cos 0 \right) =\]

\[= 2 + 2 = 4\ кв.\ ед.\]

\[\textbf{в)}\ y = \cos x;\]

\[x = \frac{\pi}{2};\ \ x = \frac{3\pi}{2};\ \ y = 0;\]

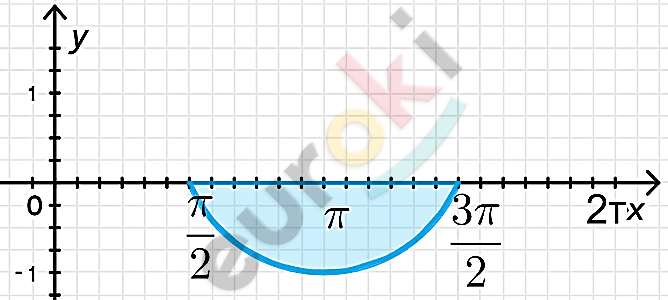
\[S = - \int_{\frac{\pi}{2}}^{\frac{3\pi}{2}}{\cos x\text{dx}} = - \left. \ \sin x \right|_{\frac{\pi}{2}}^{\frac{3\pi}{2}} =\]

\[= - \sin\left( \frac{3\pi}{2} \right) + \sin\frac{\pi}{2} = 1 + 1 =\]

\[= 2\ кв.\ ед.\]

\[\textbf{г)}\ y = \cos x;\]

\[x = 0;\ \ x = 2\pi;\ \ y = 0;\]

\[Фигуру\ можно\ разделить\ \]

\[на\ 4\ равные\ части:\]

\[S = 4\int_{0}^{\frac{\pi}{2}}{\cos x\text{dx}} = 4\left. \ \sin x \right|_{0}^{\frac{\pi}{2}} =\]

\[= 4\left( \sin\frac{\pi}{2} - \sin 0 \right) = 4 \cdot 1 =\]

\[= 4\ кв.\ ед.\]