Решебник по алгебре 11 класс Никольский Параграф 11. Равносильность неравенств на множествах Задание 50
Задание 50
\[\boxed{\mathbf{50.}}\]
\[\textbf{а)}\ x^{4} + x^{3} + x^{2} - 3x > 0\]
\[M = \lbrack - 2;2\rbrack.\]
\[x^{4} + x^{3} + x^{2} - x - x - x > 0\]

\[x(x - 1)\left( x^{2} + 2x + 3 \right) > 0\]
\[x^{2} + 2x + 3 = 0\]
\[D_{1} = 1 - 3 = - 2 < 0\]
\[нет\ корней.\]
\[x(x - 1) > 0\]
\[x < 0;\ \ x > 1.\]
\[- 2 \leq x \leq 2:\]
\[x \in \lbrack - 2;0) \cup (1;2\rbrack.\]
\[Ответ:x \in \lbrack - 2;0) \cup (1;2\rbrack.\]
\[\textbf{б)}\ x^{4} + x^{3} + x^{2} - 14x < 0\]
\[M = \lbrack 1;3\rbrack.\]
\[x\left( x^{3} + x^{2} + x - 14 \right) < 0\]
\[x = 2 - корень\ трехчлена:\]

\[x^{3} + x^{2} + x - 14 =\]
\[= (x - 2)\left( x^{2} + 3x + 7 \right)\]
\[x(x - 2)\left( x^{2} + 3x + 7 \right) < 0\]
\[x^{2} + 3x + 7 = 0\]
\[D = 9 - 28 = - 19 < 0\]
\[\left( x^{2} + 3x + 7 \right) > 0\ при\ любом\ \text{x.}\]
\[x(x - 2) < 0\]
\[0 < x < 2.\]
\[1 \leq x \leq 3:\]
\[x \in \lbrack 1;2).\]
\[Ответ:x \in \lbrack 1;2).\]
\[\boxed{\mathbf{51.}}\]
\[\textbf{а)}\ \ 2\sin x\cos x + \frac{\sqrt{2}}{2} > \cos x + \sqrt{2}\sin x;\ \ \left\lbrack \frac{2\pi}{3};\frac{4\pi}{3} \right\rbrack\]
\[2\sin x\cos x + \frac{\sqrt{2}}{2} - \cos x - \sqrt{2}\sin x > 0\]
\[\cos x\left( 2\sin x - 1 \right) - \frac{\sqrt{2}}{2}\left( 2\sin x - 1 \right) > 0\]
\[\left( 2\sin x - 1 \right)\left( \cos x - \frac{\sqrt{2}}{2} \right) > 0\]
\[1)\ \left\{ \begin{matrix} 2\sin x - 1 > 0 \\ \cos x - \frac{\sqrt{2}}{2} > 0 \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} \sin x > \frac{1}{2}\text{\ \ \ } \\ \cos x > \frac{\sqrt{2}}{2} \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} \frac{\pi}{6} + 2\pi k < x < \frac{5\pi}{6} + 2\pi k \\ - \frac{\pi}{4} + 2\pi n < x < \frac{\pi}{4} + 2\pi n \\ \end{matrix} \right.\ \]
\[2)\ \left\{ \begin{matrix} 2\sin x - 1 < 0 \\ \cos x - \frac{\sqrt{2}}{2} < 0 \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} \sin x < \frac{1}{2}\text{\ \ \ } \\ \cos x < \frac{\sqrt{2}}{2} \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} \frac{5\pi}{6} + 2\pi k < x < \frac{13\pi}{6} + 2\pi k \\ \frac{\pi}{4} + 2\pi n < x < \frac{7\pi}{4} + 2\pi n\ \ \ \ \\ \end{matrix} \right.\ \]
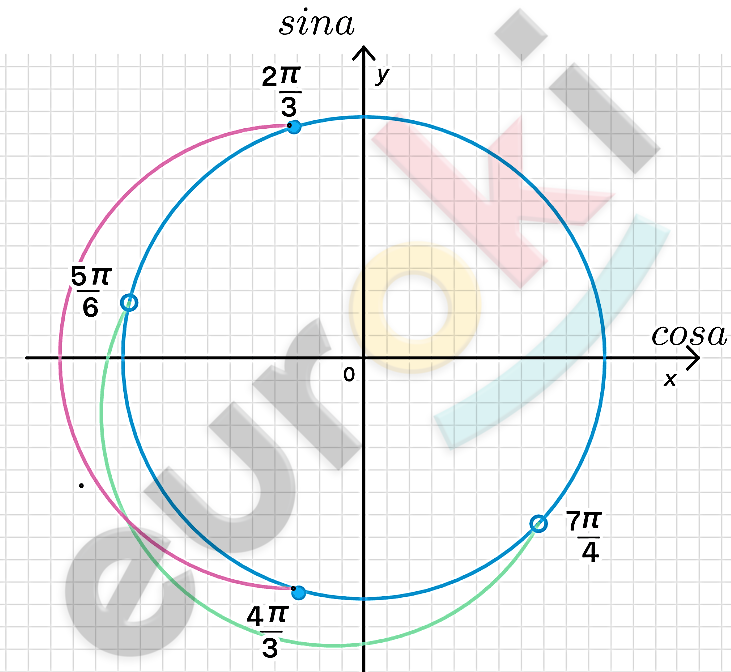
\[Равносильно\ совокупности:\]
\[\left\{ \begin{matrix} \frac{\pi}{6} + 2\pi n < x < \frac{\pi}{4} + 2\pi n\ \ \ \ \ \\ \frac{5\pi}{6} + 2\pi k < x < \frac{7\pi}{4} + 2\pi k \\ \end{matrix} \right.\ \]
\[Промежутку\ принадлежат\ решения:\]
\[\frac{5\pi}{6} < x \leq \frac{4\pi}{3}.\]
\[Ответ:x \in \left( \frac{5\pi}{6};\ \frac{4\pi}{3} \right\rbrack.\]
\[\textbf{б)}\sin{2x} - \frac{\sqrt{3}}{2} < \sqrt{3}\sin x - \cos x;\ \ \lbrack 0;\ \pi\rbrack\]
\[2\sin x\cos x - \frac{\sqrt{3}}{2} - \sqrt{3}\sin x + \cos x < 0\]
\[\cos x\left( 2\sin x + 1 \right) - \frac{\sqrt{3}}{2}\left( 1 + 2\sin x \right) < 0\]
\[\left( 1 + 2\sin x \right)\left( \cos x - \frac{\sqrt{3}}{2} \right) < 0\]
\[1)\ \left\{ \begin{matrix} 1 + 2\sin x < 0 \\ \cos x - \frac{\sqrt{3}}{2} > 0 \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} \sin x < - \frac{1}{2} \\ \cos x > \frac{\sqrt{3}}{5} \\ \end{matrix} \right.\ \]
\[2)\ \left\{ \begin{matrix} 1 + 2\sin x > 0 \\ \cos x - \frac{\sqrt{3}}{2} < 0 \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} \sin x > - \frac{1}{2} \\ \cos x < \frac{\sqrt{3}}{5} \\ \end{matrix} \right.\ \]

\[Равносильно\ совокупности\ систем:\]
\[\left\{ \begin{matrix} x = \varnothing\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \frac{\pi}{6} + 2\pi k < x < \frac{7\pi}{6} + 2\pi k \\ \end{matrix} \right.\ \]
\[Промежутку\ принадлежат\ решения:\]
\[\frac{\pi}{6} < x \leq \pi.\]
\[Ответ:\ x \in \left( \frac{\pi}{6};\pi \right\rbrack.\]
\[\boxed{\mathbf{52.}}\]
\[\textbf{а)}\sin\frac{\text{πx}}{2} + \sqrt{3}\cos\frac{\text{πx}}{4} + \sin\frac{\text{πx}}{4} + \frac{\sqrt{3}}{2} > 0;\ \ \lbrack - 1;5\rbrack\]
\[2\sin\frac{\text{πx}}{4}\cos\frac{\text{πx}}{4} + \sqrt{3}\cos\frac{\text{πx}}{4} + \sin\frac{\text{πx}}{4} + \frac{\sqrt{3}}{2} > 0\]
\[\sin\frac{\text{πx}}{4}\left( 2\cos\frac{\text{πx}}{4} + 1 \right) + \frac{\sqrt{3}}{2}\left( 2\cos\frac{\text{πx}}{4} + 1 \right) > 0\]
\[\left( 2\cos\frac{\text{πx}}{4} + 1 \right)\left( \sin\frac{\text{πx}}{4} + \frac{\sqrt{3}}{2} \right) > 0\]
\[1)\ \left\{ \begin{matrix} 2\cos\frac{\text{πx}}{4} + 1 > 0 \\ \sin\frac{\text{πx}}{4} + \frac{\sqrt{3}}{2} > 0\ \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} \cos\frac{\text{πx}}{4} > - \frac{1}{2}\text{\ \ } \\ \sin\frac{\text{πx}}{4} > - \frac{\sqrt{3}}{2} \\ \end{matrix}\ \right.\ \]
\[2)\ \left\{ \begin{matrix} 2\cos\frac{\text{πx}}{4} + 1 < 0 \\ \sin\frac{\text{πx}}{4} + \frac{\sqrt{3}}{2} < 0\ \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} \cos\frac{\text{πx}}{4} < - \frac{1}{2}\text{\ \ } \\ \sin\frac{\text{πx}}{4} < - \frac{\sqrt{3}}{2} \\ \end{matrix}\ \right.\ \]
\[- \frac{\pi}{3} + 2\pi k < \frac{\text{πx}}{4} < \frac{2\pi}{3} + 2\pi k\]
\[- \frac{4}{3} + 8k < x < \frac{8}{3} + 8k.\]
\[Промежутку\ принадлежат\ решения:\]
\[- 1 \leq x < \frac{8}{3}.\]
\[Ответ:x \in \left\lbrack - 1;\frac{8}{3} \right).\]
\[\textbf{б)}\sin\frac{\text{πx}}{3} + \sqrt{2}\cos\frac{\text{πx}}{6} + \sqrt{3}\sin\frac{\text{πx}}{6} + \frac{\sqrt{6}}{2} < 0;\ \lbrack 5;13\rbrack\]
\[2\sin\frac{\text{πx}}{6}\cos\frac{\text{πx}}{6} + \sqrt{2}\cos\frac{\text{πx}}{6} + \sqrt{3}\sin\frac{\text{πx}}{6} + \frac{\sqrt{6}}{2} < 0\]
\[2\sin\frac{\text{πx}}{6}\left( \cos\frac{\text{πx}}{6} + \frac{\sqrt{3}}{2} \right) + \sqrt{2}\left( \cos\frac{\text{πx}}{6} + \frac{\sqrt{3}}{2} \right) < 0\]
\[\left( \cos\frac{\text{πx}}{6} + \frac{\sqrt{3}}{2} \right)\left( 2\sin\frac{\text{πx}}{6} + \sqrt{2} \right) < 0\]
\[1)\ \left\{ \begin{matrix} \cos\frac{\text{πx}}{6} + \frac{\sqrt{3}}{2} < 0\ \ \ \\ 2\sin\frac{\text{πx}}{6} + \sqrt{2} > 0 \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} \cos\frac{\text{πx}}{6} < - \frac{\sqrt{3}}{2} \\ \sin\frac{\text{πx}}{6} > - \frac{\sqrt{2}}{2} \\ \end{matrix} \right.\ \]
\[2)\ \left\{ \begin{matrix} \cos\frac{\text{πx}}{6} + \frac{\sqrt{3}}{2} > 0\ \ \ \\ 2\sin\frac{\text{πx}}{6} + \sqrt{2} < 0 \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} \cos\frac{\text{πx}}{6} > - \frac{\sqrt{3}}{2} \\ \sin\frac{\text{πx}}{6} < - \frac{\sqrt{2}}{2} \\ \end{matrix} \right.\ \]
\[- \frac{3\pi}{4} + 2\pi k < \frac{\text{πx}}{6} < - \frac{\pi}{4} + 2\pi k\]
\[- \frac{9}{2} + 12k < x < - \frac{3}{2} + 12k.\]
\[Промежутку\ принадлежат\ решения:\]
\[7,5 < x < 10,5.\]
\[При\ k = 1:\]
\[\frac{5\pi}{6} + 2\pi n < \frac{\text{πx}}{6} < \frac{7\pi}{6} + 2\pi n\]
\[5 + 12n < x < 7 + 12n.\]
\[Промежутку\ принадлежат\ решения:\]
\[5 < x < 7.\]
\[Объединим:\]
\[x \in (5;7) \cup (7,5;10,5).\]
\[Ответ:\ x \in (5;7) \cup (7,5;10,5).\]
\[\boxed{\mathbf{53.}}\]
\[\textbf{а)}\ \sqrt{\text{si}n^{2}x + \sin{2x} - 3cos^{2}x} > \cos x - \sin x;\left( \frac{\pi}{4};\frac{5\pi}{4} \right)\]
\[Для\ каждого\ значения\ из\ данного\ промежутка\ справедливо:\]
\[\cos x - \sin x < 0.\]
\[\text{si}n^{2} + \sin{2x} - 3cos^{2}x \geq 0\]
\[\text{si}n^{2}x + 2\sin x\cos x - 3cos^{2}x \geq 0\]
\[\text{si}n^{2}x - \cos^{2}x + 2\sin x\cos x - 2cos^{2}x \geq 0\]
\[\left( \sin x + \cos x \right)\left( \sin x - \cos x \right) + 2\cos x\left( \sin x - \cos x \right) \geq 0\]
\[\left( \sin x - \cos x \right)\left( \sin x + \cos x + 2\cos x \right) \geq 0\]
\[\left( \sin x + 3\cos x \right)\left( \sin x - \cos x \right) \geq 0\]
\[\sin x - \cos x > 0\ при\ x \in M.\]
\[\sin x + 3\cos x \geq 0\]
\[a = \arcsin\frac{3}{\sqrt{10}} - вспомогательный\ угол.\]
\[\sin(x + a) \geq 0\]
\[2\pi k - a \leq a \leq \pi - a + 2\pi k;\ \ k \in Z;\]
\[Промежутку\ принадлежат\ решения:\]
\[\frac{\pi}{4} < x \leq \pi - \arcsin\frac{3}{\sqrt{10}}.\]
\[Ответ:x \in \left( \frac{\pi}{4};\ \pi - \arcsin\frac{3}{\sqrt{10}} \right).\]
\[\textbf{б)}\ \sqrt{\text{si}n^{2}x - 2\sin{2x} + 3cos^{2}x} > \sin x - \cos x;\left( \frac{5\pi}{4};\frac{9\pi}{4} \right)\]
\[\text{si}n^{2}x - 2\sin{2x} + 3cos^{2}x > \left( \sin x - \cos x \right)^{2}\]
\[\text{si}n^{2}x - 2\sin{2x} + 3\cos^{2}x > sin^{2}x - 2\sin x\cos x + \cos^{2}x\]



\[\frac{3\pi}{2} + 2\pi k < x < \frac{9\pi}{4} + \pi k.\]
\[Нет\ решений,\ удовлетворяющих\ промежутку.\]

\[\frac{\pi}{2} + \pi k < x < \frac{5\pi}{4} + \pi k.\]
\[Нет\ решений,\ удовлетворяющих\ промежутку.\]
\[1)\ sin^{2}x - 2\sin{2x} + 3cos^{2}x \geq 0\]

\[\text{co}s^{2}x \geq 0\ при\ любом\ x;\]
\[tg^{2}x - 4tgx + 3 \geq 0\]
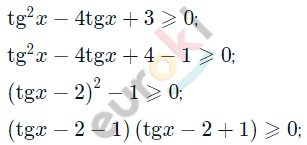
\[(tgx - 3)(tgx - 1) \geq 0\]
\[tgx \geq 3\]
\[x \geq arctg\ 3 + \pi k.\ \]
\[tgx \leq 1\]
\[x \leq \frac{\pi}{4} + \pi k.\]
\[Промежутку\ принадлежат\ значения:\]
\[arctg\ 3 + \pi k \leq x \leq \frac{\pi}{4} + \pi k.\]
\[x \in \left( arctg\ 3 + \pi;\frac{5\pi}{4} \right)\ при\ k = 1.\]
\[Ответ:x \in \left( arctg\ 3 + \pi;\frac{5\pi}{4} \right)\ при\ k = 1.\]
\[\boxed{\mathbf{54.}}\]
\[\textbf{а)}\cos{3x} > \left| \cos x \right|;\ \ \ \left\lbrack - \frac{5\pi}{6};\frac{5\pi}{6} \right\rbrack\]
\[1)\ \cos{3x} \geq 0\]
\[- \frac{\pi}{2} + 2\pi k \leq 3x \leq \frac{\pi}{2} + 2\pi k\]
\[- \frac{\pi}{6} + \frac{2\pi k}{3} \leq x \leq \frac{\pi}{6} + \frac{2\pi k}{3}.\]
\[2)\ |\cos x|\]



\[x \in \left( - \pi + 2\pi k;\ - \frac{\pi}{2} + 2\pi k \right);\]
\[x \in \left( \frac{\pi}{2} + 2\pi k;\ \pi + 2\pi k \right).\]


\[x \in \left( - \frac{\pi}{4} + 2\pi k;\frac{\pi}{4} + 2\pi k \right);\]
\[x \in \left( \frac{\pi}{2} + 2\pi k;\frac{3\pi}{4} + 2\pi k \right) \cup \left( \frac{5\pi}{4} + 2\pi k;\frac{3\pi}{2} + 2\pi k \right).\]
\[Множество\ решений\ неравенств:\]

\[Решение\ на\ промежутке:\]

\[Ответ:\ \]

\[\textbf{б)}\sin{3x} > \left| \sin x \right|;\ \ \ \left\lbrack - \frac{3\pi}{2};\frac{\pi}{2} \right\rbrack\]
\[1)\ \sin{3x} < 0 - нет\ решений.\]
\[\sin{3x} \geq 0\]
\[2\pi k \leq 3x \leq \pi + 2\pi k\]
\[\frac{2\pi k}{3} \leq x \leq \frac{\pi}{3} + \frac{2\pi k}{3}.\]
\[2)\ \left| \sin x \right|\]
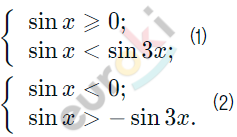



\[x \in \left( - \frac{3\pi}{4} + 2\pi k;\ - \frac{\pi}{4} + 2\pi k \right).\]




\[k = 0:\]
\[0 < x < \frac{\pi}{4}.\]
\[k = - 1:\]
\[- \frac{5\pi}{4} < x < - \pi.\]
\[Решение\ неравенства\ на\ промежутке:\]
\[x \in \left( - \frac{5\pi}{4}; - \pi \right) \cup \left( 0;\frac{\pi}{4} \right).\]
\[Ответ:x \in \left( - \frac{5\pi}{4}; - \pi \right) \cup \left( 0;\frac{\pi}{4} \right).\]
\[\boxed{\mathbf{55.}}\]
\[\textbf{а)}\ \left( x^{2} - 4x + 3 \right)\sqrt{x - 2} \geq 0\]
\[x - 2 \geq 0\]
\[x \geq 2.\]
\[M = \lbrack 2; + \infty).\]
\[x^{2} - 4x + 3 \geq 0\]
\[D_{1} = 4 - 3 = 1\]
\[x_{1} = 2 + 1 = 3;\]
\[x_{2} = 2 - 1 = 1;\]
\[(x - 1)(x - 3) \geq 0\]
\[x \leq 1;\ \ x \geq 3.\]
\[x \in \left\{ 2 \right\} \cup \lbrack 3; + \infty).\]
\[Ответ:x \in \left\{ 2 \right\} \cup \lbrack 3; + \infty).\]
\[\textbf{б)}\ \left( x^{2} - 3x - 10 \right)\sqrt{3 - x} \geq 0\]
\[3 - x \geq 0\]
\[x \leq 3.\]
\[M = ( - \infty;3\rbrack.\]
\[x^{2} - 3x - 10 \geq 0\]
\[x_{1} + x_{2} = 3;\ \ \ x_{1} \cdot x_{2} = - 10\]
\[x_{1} = - 2;\ \ \ x_{2} = 5;\]
\[(x + 2)(x - 5) \geq 0\]
\[x \leq - 2;\ \ x \geq 5.\]
\[x \in ( - \infty; - 2\rbrack \cup \left\{ 3 \right\}.\]
\[Ответ:\ x \in ( - \infty; - 2\rbrack \cup \left\{ 3 \right\}.\]
\[\textbf{в)}\ \left( x^{2} - 2x - 15 \right)\sqrt{x + 4} \leq 0\]
\[x + 4 \geq 0\]
\[x \geq - 4.\]
\[M = \lbrack - 4; + \infty).\]
\[x^{2} - 2x - 15 \leq 0\]
\[D_{1} = 1 + 15 = 16\]
\[x_{1} = 1 + 4 = 5;\]
\[x_{2} = 1 - 4 = - 3;\]
\[(x + 3)(x - 5) \leq 0\]
\[- 3 \leq x \leq 5.\]
\[x \in \lbrack - 3;5\rbrack \cup \left\{ 4 \right\}.\]
\[Ответ:\ x \in \lbrack - 3;5\rbrack \cup \left\{ 4 \right\}.\]
\[\textbf{г)}\ \left( x^{2} + x - 6 \right)\sqrt{x + 5} \leq 0\]
\[x + 5 \geq 0\]
\[x \geq - 5.\]
\[M = \lbrack - 5; + \infty).\]
\[x^{2} + x - 6 \leq 0\]
\[x_{1} + x_{2} = - 1;\ \ x_{1} \cdot x_{2} = - 6\]
\[x_{1} = - 3;\ \ \ x_{2} = 2.\]
\[(x + 3)(x - 2) \leq 0\]
\[- 3 \leq x \leq 2.\]
\[x \in \lbrack - 3;2\rbrack \cup \left\{ - 5 \right\}.\]
\[Ответ:\ x \in \lbrack - 3;2\rbrack \cup \left\{ - 5 \right\}.\]
\[\boxed{\mathbf{56.}}\]
\[\textbf{а)}\ \sqrt{x^{2} - 9}(x + 8) \geq 0\]
\[x^{2} - 9 \geq 0\]
\[x^{2} \geq 9\]
\[x \leq - 3;\ \ x \geq 3.\]
\[M = ( - \infty; - 3\rbrack \cup \lbrack 3; + \infty).\]
\[x + 8 \geq 0\]
\[x \geq - 8.\]
\[x \in \lbrack - 8; - 3\rbrack \cup \lbrack 3; + \infty).\]
\[Ответ:x \in \lbrack - 8; - 3\rbrack \cup \lbrack 3; + \infty).\]
\[\textbf{б)}\ (x - 4)\sqrt{x^{2} - 4} \leq 0\]
\[x^{2} - 4 \geq 0\]
\[x^{2} \geq 4\]
\[x \leq - 2;\ \ x \geq 2.\]
\[M = ( - \infty; - 2\rbrack \cup \lbrack 2; + \infty).\]
\[x - 4 \leq 0\]
\[x \leq 4.\]
\[x \in ( - \infty; - 2\rbrack \cup \lbrack 2;4\rbrack.\]
\[Ответ:x \in ( - \infty; - 2\rbrack \cup \lbrack 2;4\rbrack.\]
\[\textbf{в)}\ \sqrt{x^{2} - 16}(x - 5) \geq 0\]
\[x^{2} - 16 \geq 0\]
\[x^{2} \geq 16\]
\[x \leq - 4;\ \ x \geq 4.\]
\[M = ( - \infty; - 4\rbrack \cup \lbrack 4; + \infty).\]
\[x - 5 \geq 0\]
\[x \geq 5.\]
\[x \in \left\{ - 4 \right\} \cup \left\{ 4 \right\} \cup \lbrack 5; + \infty).\]
\[Ответ:x \in \left\{ - 4 \right\} \cup \left\{ 4 \right\} \cup \lbrack 5; + \infty)\text{.\ }\]
\[\textbf{г)}\ (x + 7)\sqrt{x^{2} - 25} \leq 0\]
\[x^{2} - 25 \geq 0\]
\[x^{2} \geq 25\]
\[x \leq - 5;\ \ x \geq 5.\]
\[M = ( - \infty; - 5\rbrack \cup \lbrack 5; + \infty).\]
\[x + 7 \leq 0\]
\[x \leq - 7.\]
\[x \in ( - \infty; - 7\rbrack \cup \left\{ - 5 \right\} \cup \left\{ 5 \right\}.\]
\[Ответ:x \in ( - \infty; - 7\rbrack \cup \left\{ - 5 \right\} \cup \left\{ 5 \right\}.\]
\[\boxed{\mathbf{57.}}\]
\[\textbf{а)}\ \frac{\sqrt{12 - x - x^{2}}}{2x + 7} \leq \frac{\sqrt{12 - x - x^{2}}}{x - 5}\]
\[2x + 7 \neq 0\]
\[2x \neq - 7\]
\[x \neq - 3,5.\]
\[x - 5 \neq 0\]
\[x \neq 5.\]
\[12 - x - x^{2} \geq 0\]
\[x^{2} + x - 12 \leq 0\]
\[x_{1} + x_{2} = - 1;\ \ x_{1} \cdot x_{2} = - 12\]
\[x_{1} = - 4;\ \ x_{2} = 3;\]
\[(x + 4)(x - 3) \leq 0\]
\[- 4 \leq x \leq 3.\]
\[M = \lbrack - 4;\ - 3,5) \cup ( - 3,5;3\rbrack.\]
\[2x + 7 \geq x - 5\]
\[x \geq - 12.\]
\[x \in \lbrack - 4; - 3,5) \cup \left\{ 3 \right\}.\]
\[Ответ:x \in \lbrack - 4; - 3,5) \cup \left\{ 3 \right\}.\]
\[\textbf{б)}\ \frac{\sqrt{8 - 2x - x^{2}}}{2x + 9} \geq \frac{\sqrt{8 - 2x - x^{2}}}{x - 5}\]
\[2x + 9 \neq 0\]
\[2x \neq - 9\]
\[x \neq - 4,5.\]
\[x - 5 \neq 0\]
\[x \neq 5.\]
\[8 - 2x - x^{2} \geq 0\]
\[x^{2} + 2x - 8 \leq 0\]
\[D_{1} = 1 + 8 = 9\]
\[x_{1} = - 1 + 3 = 2;\]
\[x_{2} = - 1 - 3 = - 4;\]
\[(x + 4)(x - 2) \leq 0\]
\[- 4 \leq x \leq 2.\]
\[M = \lbrack - 4;2\rbrack.\]
\[2x + 9 \leq x - 5\]
\[x \leq - 14.\ \]
\[x \in \lbrack - 4;2\rbrack.\]
\[Ответ:x \in \lbrack - 4;2\rbrack.\]
\[\textbf{в)}\ \frac{\sqrt{18 - 3x - x^{2}}}{x - 2} \leq \frac{\sqrt{18 - 3x - x^{2}}}{2x + 3}\]
\[x - 2 \neq 0\]
\[x \neq 2.\]
\[2x + 3 \neq 0\]
\[x \neq - 1,5.\]
\[18 - 3x - x^{2} \geq 0\]
\[x^{2} + 3x - 18 \leq 0\]
\[x_{1} + x_{2} = - 3;\ \ x_{1} \cdot x_{2} = - 18\]
\[x_{1} = - 6;\ \ x_{2} = 3;\]
\[(x + 6)(x - 3) \leq 0\]
\[- 6 \leq x \leq 3.\]
\[M = \lbrack - 6; - 1,5) \cup ( - 1,5;2) \cup (2;3\rbrack.\]
\[x - 2 \geq 2x + 3\]
\[- x \geq 5\]
\[x \leq - 5.\]
\[x \in \{ - 6\} \cup \lbrack - 5; - 1,5) \cup ( - 1,5;2) \cup (2;3\rbrack.\]
\[Ответ:x \in \{ - 6\} \cup \lbrack - 5; - 1,5) \cup ( - 1,5;2) \cup (2;3\rbrack.\]
\[\textbf{г)}\ \frac{\sqrt{6 + x - x^{2}}}{2x + 5} \geq \frac{\sqrt{6 + x - x^{2}}}{x + 4}\]
\[2x + 5 \neq 0\]
\[2x \neq - 5\]
\[x \neq - 2,5.\]
\[x + 4 \neq 0\]
\[x \neq - 4.\]
\[6 + x - x^{2} \geq 0\]
\[x^{2} - x - 6 \leq 0\]
\[x_{1} + x_{2} = 1;\ \ x_{1} \cdot x_{2} = - 6\]
\[x_{1} = - 2;\ \ x_{2} = 3;\]
\[(x + 2)(x - 3) \leq 0\]
\[- 2 \leq x \leq 3.\]
\[M = \lbrack - 2;3\rbrack.\]
\[2x + 5 \leq x + 4\]
\[x \leq - 1.\]
\[x \in \lbrack - 2; - 1\rbrack \cup \left\{ 3 \right\}.\]
\[Ответ:x \in \lbrack - 2; - 1\rbrack \cup \left\{ 3 \right\}.\]
\[\boxed{\mathbf{58.}}\]
\[\textbf{а)}\ \frac{(2x + 3)\sqrt{x - 2}}{x - 6,6} \geq \frac{5\sqrt{x - 2}}{x - 5}\]
\[x - 6,6 \neq 0\]
\[x \neq 6,6.\]
\[x - 5 \neq 0\]
\[x \neq 5.\]
\[x - 2 \geq 0\]
\[x \geq 2.\]
\[M = \lbrack 2;5) \cup (5;6,6) \cup (6,6; + \infty).\]
\[\sqrt{x - 2}\left( \frac{(2x + 3)(x - 5) - 5(x - 6,6)}{(x - 6,6)(x - 5)} \right) \geq 0\]
\[\sqrt{x - 2}\left( \frac{2x^{2} + 3x - 10x - 15 - 5x + 33}{(x - 6,6)(x - 5)} \right) \geq 0\]
\[\sqrt{x - 2} \cdot \frac{2x^{2} - 12x + 18}{(x - 6,6)(x - 5)} \geq 0\]
\[2\sqrt{x - 2} \cdot \frac{x^{2} - 6x + 9}{(x - 6,6)(x - 5)} \geq 0\]
\[\frac{2\sqrt{x - 2}(x - 3)^{2}}{(x - 6,6)(x - 5)} \geq 0\]
\[x = 2;\ \ x = 3.\]
\[2\sqrt{x - 2}(x - 3)^{2} \geq 0\ при\ \text{M.}\]
\[(x - 6,6)(x - 5) > 0\]
\[x < 5;\ \ x > 6,6.\]
\[Решение\ неравенства:\]
\[x \in \lbrack 2;5) \cup (6,6; + \infty).\]
\[Ответ:x \in \lbrack 2;5) \cup (6,6; + \infty).\]
\[\textbf{б)}\ \frac{3x + 1}{(2x + 1)\sqrt{2 - x}} \leq \frac{1}{(x + 1)\sqrt{2 - x}}\]
\[2x + 1 \neq 0\]
\[2x \neq - 1\]
\[x \neq - 0,5.\]
\[x + 1 \neq 0\]
\[x \neq - 1.\]
\[2 - x > 0\]
\[x < 2.\]
\[M = ( - \infty; - 1) \cup ( - 1; - 0,5) \cup ( - 0,5;2).\]
\[\frac{1}{\sqrt{2 - x}}\left( \frac{3x + 1}{2x + 1} - \frac{1}{x + 1} \right) \leq 0\]
\[\frac{1}{\sqrt{2 - x}}\left( \frac{(3x + 1)(x + 1) - (2x + 1)}{(2x + 1)(x + 1)} \right) \leq 0\]
\[\frac{1}{\sqrt{2 - x}}\left( \frac{3x^{2} + x + 3x + 1 - 2x - 1}{(2x + 1)(x + 1)} \right) \leq 0\]
\[\frac{1}{\sqrt{2 - x}}\left( \frac{3x^{2} + 2x}{(2x + 1)(x + 1)} \right) \leq 0\]
\[\frac{1}{\sqrt{2 - x}} \cdot \frac{x(x + 2)}{(2x + 1)(x + 1)} \leq 0\]
\[x = 0;\ \ x = - \frac{2}{3}.\]
\[1)\ \left\{ \begin{matrix} 3x\left( x + \frac{2}{3} \right) < 0\ \ \ \ \ \ \ \ \\ (2x + 1)(x + 1) > 0 \\ \end{matrix} \right.\ \]
\[- 0,5 < x < 0.\]
\[2)\ \left\{ \begin{matrix} 3x\left( x + \frac{2}{3} \right) > 0\ \ \ \ \ \ \ \ \ \ \\ (2x + 1)(x + 1) < 0 \\ \end{matrix} \right.\ \]
\[- 1 < x < - \frac{2}{3}.\]
\[Решение\ неравенства:\]
\[x \in \left( - 1; - \frac{2}{3} \right\rbrack \cup ( - 0,5;0\rbrack.\]
\[Ответ:x \in \in \left( - 1; - \frac{2}{3} \right\rbrack \cup ( - 0,5;0\rbrack.\]
\[\textbf{в)}\ \frac{(2x - 7)\sqrt{x - 1}}{x - 3} \geq \frac{9\sqrt{x - 1}}{5 - x}\]
\[x - 3 \neq 0\]
\[x \neq 3.\]
\[5 - x \neq 0\]
\[x \neq 5.\]
\[x - 1 \geq 0\]
\[x \geq 1.\]
\[M = \lbrack 1;3) \cup (3;5) \cup (5; + \infty).\]
\[\sqrt{x - 1}\left( \frac{2x - 7}{x - 3} - \frac{9}{5 - x} \right) \geq 0\]
\[\sqrt{x - 1}\left( \frac{(2x - 7)(5 - x) - 9(x - 3)}{(x - 3)(5 - x)} \right) \geq 0\]
\[\sqrt{x - 1}\left( \frac{10x - 35 - 2x^{2} + 7x - 9x + 27}{(x - 3)(5 - x)} \right) \geq 0\]
\[\sqrt{x - 1}\left( \frac{- 2x^{2} + 8x - 8}{(x - 3)(5 - x)} \right) \geq 0\]
\[- 2\sqrt{x - 1} \cdot \frac{x^{2} - 4x + 4}{(x - 3)(5 - x)} \geq 0\]
\[\frac{\sqrt{x - 1}(x - 2)^{2}}{(x - 3)(5 - x)} \leq 0\]
\[(x - 3)(5 - x) < 0\]
\[x < 3;\ \ x > 5.\]
\[Решение\ неравенства:\]
\[x \in \lbrack 1;3) \cup (5; + \infty).\]
\[Ответ:x \in \lbrack 1;3) \cup (5; + \infty)\]
\[\textbf{г)}\ \frac{1}{(x + 1)\sqrt{9 - x}} \leq \frac{4 - x}{(8 - x)\sqrt{9 - x}}\]
\[x + 1 \neq 0\]
\[x \neq - 1.\]
\[9 - x \geq 0\]
\[x \leq 9.\]
\[8 - x \neq 0\]
\[x \neq 8.\]
\[M = ( - \infty; - 1) \cup ( - 1;8) \cup (8;9\rbrack.\]
\[\frac{1}{\sqrt{9 - x}}\left( \frac{1}{x + 1} - \frac{4 - x}{8 - x} \right) \leq 0\]
\[\frac{1}{\sqrt{9 - x}}\left( \frac{8 - x - (4 - x)(x + 1)}{(x + 1)(8 - x)} \right) \leq 0\]
\[\frac{1}{\sqrt{9 - x}}\left( \frac{8 - x - 4x + x^{2} - 4 + x}{(x + 1)(8 - x)} \right) \leq 0\]
\[\frac{1}{\sqrt{9 - x}} \cdot \frac{x^{2} - 4x + 4}{(x + 1)(8 - x)} \leq 0\]
\[\frac{1}{\sqrt{9 - x}} \cdot \frac{(x - 2)^{2}}{(x + 1)(8 - x)} \leq 0\]
\[(x + 1)(8 - x) < 0\]
\[x < - 1;\ \ x > 8.\]
\[Решение\ неравенства:\]
\[x \in ( - \infty; - 1) \cup (8;9\rbrack.\]
\[Ответ:x \in ( - \infty; - 1) \cup (8;9\rbrack.\]
\[\boxed{\mathbf{59.}}\]
\[\textbf{а)}\ 0,065 \cdot 4^{x} \leq 64^{\frac{1}{x}}\]
\[x \neq 0;\]
\[M = ( - \infty;0) \cup (0; + \infty).\]
\[\frac{1}{16} \cdot 4^{x} \leq \left( 4^{3} \right)^{\frac{1}{x}}\]
\[4^{- 2} \cdot 4^{x} \leq 4^{\frac{3}{x}}\]
\[4^{- 2 + x} \leq 4^{\frac{3}{x}}\]
\[x - 2 \leq \frac{3}{x}\]
\[x^{2} - 2x - 3 \leq 0\]
\[D_{1} = 1 + 3 = 4\]
\[x_{1} = 1 + 2 = 3;\]
\[x_{2} = 1 - 2 = - 1;\]
\[(x + 1)(x - 3) \leq 0\]
\[x \leq - 1;\ \ x \geq 3.\]
\[Решение\ неравенства:\]
\[x \in ( - \infty; - 1\rbrack \cup (0;3\rbrack.\]
\[Ответ:x \in ( - \infty; - 1\rbrack \cup (0;3\rbrack.\]
\[\textbf{б)}\ 9 \cdot 3 \leq \frac{1}{9} \cdot \left( \frac{1}{27} \right)^{\frac{1}{x}}\]
\[x \neq 0;\]
\[M = ( - \infty;0) \cup (0; + \infty).\]
\[3^{2} \cdot 3 \leq 3^{- 2} \cdot \left( 3^{- 3} \right)^{\frac{1}{x}}\]
\[3^{3} \leq 3^{- 2} \cdot 3^{- \frac{3}{x}}\ \ \ \ | \cdot 3^{2}\]
\[3^{5} \leq 3^{- \frac{3}{x}}\]
\[5 \leq - \frac{3}{x}\]
\[x \geq - \frac{3}{5}.\]
\[Решение\ неравенства:\]
\[x \in \left\lbrack - \frac{3}{5};0 \right).\]
\[Ответ:x \in \left\lbrack - \frac{3}{5};0 \right).\]
\[\textbf{в)}\ 0,2 \leq \left( \frac{1}{25} \right)^{\frac{1}{x}} \cdot \left( \frac{1}{125} \right)^{\frac{1}{x^{2}}}\]
\[x \neq 0.\]
\[M = ( - \infty;0) \cup (0; + \infty).\]
\[\frac{1}{5} \leq \left( \frac{1}{5^{2}} \right)^{\frac{1}{x}} \cdot \left( \frac{1}{5^{3}} \right)^{\frac{1}{x^{2}}}\]
\[5^{- 1} \leq 5^{- \frac{2}{x}} \cdot 5^{\frac{- 3}{x^{2}}}\]
\[5^{- 1} \leq 5^{\frac{- 2x - 3}{x^{2}}}\]
\[- 1 \leq - \frac{2x + 3}{x^{2}}\]
\[\frac{2x + 3}{x^{2}} \leq 1\]
\[2x + 3 \leq x^{2}\]
\[x^{2} - 2x - 3 \geq 0\]
\[D_{1} = 1 + 3 = 4\]
\[x_{1} = 1 + 2 = 3;\]
\[x_{2} = 1 - 2 = - 1;\]
\[(x + 1)(x - 3) \geq 0\]
\[x \leq - 1;\ \ x \geq 3.\]
\[Решение\ неравенства:\]
\[x \in ( - \infty; - 1\rbrack \cup \lbrack 3; + \infty).\]
\[Ответ:x \in ( - \infty; - 1\rbrack \cup \lbrack 3; + \infty).\]
\[\textbf{г)}\ 7 \leq \left( \frac{1}{49} \right)^{\frac{2}{x}} \cdot \left( \frac{1}{343} \right)^{\frac{1}{x^{2}}}\]
\[7 \leq \left( 7^{- 2} \right)^{\frac{2}{x}} \cdot \left( 7^{- 3} \right)^{\frac{1}{x^{2}}}\]
\[7 \leq 7^{- \frac{4}{x}} \cdot 7^{- \frac{3}{x^{2}}}\]
\[7 \leq 7^{\frac{- 4x - 3}{x^{2}}}\]
\[1 \leq - \frac{4x + 3}{x^{2}}\]
\[\frac{4x + 3}{x^{2}} \leq - 1\]
\[4x + 3 \leq - x^{2}\]
\[x^{2} + 4x + 3 \leq 0\]
\[D_{1} = 4 - 3 = 1\]
\[x_{1} = - 2 + 1 = - 1;\]
\[x_{2} = - 2 - 1 = - 3;\]
\[(x + 3)(x + 1) \leq 0\]
\[- 3 \leq x \leq - 1.\]
\[Решение\ неравенства:\]
\[x \in \lbrack - 3; - 1\rbrack\]
\[Ответ:x \in \lbrack - 3; - 1\rbrack.\]
\[\boxed{\mathbf{60.}}\]
\[\textbf{а)}\ \sqrt{27} \cdot 3^{- 6x^{2}} \geq 9^{4x}\]
\[M = R.\]
\[3^{\frac{3}{2}} \cdot 3^{- 6x^{2}} \geq 3^{8x}\]
\[3^{\frac{3}{2} - 6x^{2}} \geq 3^{8x}\]
\[\frac{3}{2} - 6x^{2} \geq 8x\ \ \ | \cdot ( - 2)\]
\[12x^{2} + 16x - 3 \leq 0\]
\[D_{1} = 64 + 36 = 100\]
\[x_{1} = \frac{- 8 + 10}{12} = \frac{1}{6};\]
\[x_{2} = \frac{- 8 - 10}{12} = - \frac{18}{12} = - \frac{3}{2}.\]
\[(x + 1,5)\left( x - \frac{1}{6} \right) \leq 0\]
\[- 1,5 \leq x \leq \frac{1}{6}.\]
\[Ответ:x \in \left\lbrack - 1,5;\frac{1}{6} \right\rbrack.\]
\[\textbf{б)}\ \sqrt{32} \cdot 2^{- 4x^{2}} \geq 8^{3x}\]
\[M = R.\]
\[2^{\frac{5}{2}} \cdot 2^{- 4x^{2}} \geq 2^{9x}\]
\[2^{\frac{5}{2} - 4x^{2}} \geq 2^{9x}\]
\[\frac{5}{2} - 4x^{2} \geq 9x\]
\[4x^{2} + 9x - \frac{5}{2} \leq 0\ \ \ | \cdot 2\ \]
\[8x^{2} + 18x - 5 \leq 0\]
\[D_{1} = 81 + 40 = 121\]
\[x_{1} = \frac{- 9 + 11}{8} = \frac{2}{8} = \frac{1}{4} = 0,25;\]
\[x_{2} = \frac{- 9 - 11}{8} = - \frac{20}{8} = - \frac{5}{2} = - 2,5;\]
\[(x + 2,5)(x - 0,25) \leq 0\]
\[- 2,5 \leq x \leq 0,25.\]
\[Ответ:\ x \in \lbrack - 2,5;0,25\rbrack.\]
\[\textbf{в)}\ 4 \cdot \left( \frac{1}{2} \right)^{5x^{2}} \leq \left( \frac{1}{8} \right)^{- 3x}\]
\[M = R.\]
\[2^{2} \cdot \left( 2^{- 1} \right)^{5x^{2}} \leq \left( 2^{- 3} \right)^{- 3x}\]
\[2^{2 - 5x^{2}} \leq 2^{9x}\]
\[2 - 5x^{2} \leq 9x\]
\[5x^{2} + 9x - 2 \geq 0\]
\[D = 81 + 40 = 121\]
\[x_{1} = \frac{- 9 + 11}{10} = 0,2;\]
\[x_{2} = \frac{- 9 - 11}{10} = - 2;\]
\[(x + 2)(x - 0,2) \geq 0\]
\[x \leq - 2;\ \ x \geq 0,2.\]
\[Ответ:\ x \in ( - \infty; - 2\rbrack \cup \lbrack 0,2; + \infty).\]
\[\textbf{г)}\ 125 \cdot \left( \frac{1}{5} \right)^{x^{2}} \leq \left( \frac{1}{25} \right)^{- 4x}\]
\[M = R.\]
\[5^{3} \cdot \left( 5^{- 1} \right)^{x^{2}} \leq \left( 5^{- 2} \right)^{- 4x}\]
\[5^{3 - x^{2}} \leq 5^{8x}\]
\[3 - x^{2} \leq 8x\]
\[x^{2} + 8x - 3 \geq 0\]
\[D_{1} = 16 + 3 = 19\]
\[x_{1} = - 4 + \sqrt{19};\]
\[x_{2} = - 4 - \sqrt{19};\]
\[x \leq - 4 - \sqrt{19};\ \ x \geq - 4 + \sqrt{19}.\]
\[Ответ:\ x \in \left( - \infty; - 4 - \sqrt{19} \right\rbrack \cup \left\lbrack - 4 + \sqrt{19}; + \infty \right).\]
\[\boxed{\mathbf{61.}}\]
\[\textbf{а)}\lg x + \lg{(x + 3)} \leq 1\]
\[M = (0; + \infty).\]
\[x(x + 3) \leq 10\]
\[x^{2} + 3x - 10 \leq 0\]
\[x_{1} + x_{2} = - 3;\ \ x_{1} \cdot x_{2} = - 10\]
\[x_{1} = - 5;\ \ x_{2} = 2;\]
\[(x + 5)(x - 2) \leq 0\]
\[- 5 \leq x \leq 2.\]
\[Решение\ неравенства:\]
\[x \in (0;2\rbrack.\]
\[Ответ:\ x \in (0;2\rbrack.\]
\[\textbf{б)}\log_{\frac{1}{9}}{(x + 8)} + \log_{\frac{1}{9}}x \geq - 1\]
\[M = (0; + \infty).\]
\[(x + 8) \cdot x \leq 9\]
\[x^{2} + 8x - 9 \leq 0\]
\[D_{1} = 16 + 9 = 25\]
\[x_{1} = - 4 + 5 = 1;\]
\[x_{2} = - 4 - 5 = - 9;\]
\[(x + 9)(x - 1) \leq 0\]
\[- 9 \leq x \leq 1.\]
\[Решение\ неравенства:\]
\[x \in (0;1\rbrack.\]
\[Ответ:\ x \in (0;1\rbrack.\]
\[\textbf{в)}\log_{2}x + \log_{2}{(x - 2)} \leq 3\]
\[M = (2; + \infty).\]
\[x(x - 2) \leq 8\]
\[x^{2} - 2x - 8 \leq 0\]
\[D_{1} = 1 + 8 = 9\]
\[x_{1} = 1 + 3 = 4;\]
\[x_{2} = 1 - 3 = - 2;\]
\[(x + 2)(x - 4) \leq 0\]
\[- 2 \leq x \leq 4.\]
\[Решение\ неравенства:\]
\[x \in (2;4\rbrack.\]
\[Ответ:\ x \in (2;4\rbrack.\]
\[\textbf{г)}\log_{\frac{1}{3}}{(x + 6)} + \log_{\frac{1}{3}}x \geq - 3\]
\[M = (0; + \infty).\]
\[(x + 6) \cdot x \leq 27\]
\[x^{2} + 6x - 27 \leq 0\]
\[D_{1} = 9 + 27 = 36\]
\[x_{1} = - 3 + 6 = 3;\]
\[x_{2} = - 3 - 6 = - 9;\]
\[(x + 9)(x - 3) \leq 0\]
\[- 9 \leq x \leq 3.\]
\[Решение\ неравенства:\]
\[x \in (0;3\rbrack.\]
\[Ответ:\ x \in (0;3\rbrack.\]
\[\boxed{\mathbf{62.}}\]
\[\textbf{а)}\ \frac{\sqrt{11x + 5}}{|x - 20|} \geq \frac{\sqrt{10x + 13}}{|x - 20|}\]
\[x - 20 \neq 0\]
\[x \neq 20.\]
\[11x + 5 \geq 0\]
\[11x \geq - 5\]
\[x \geq - \frac{5}{11}.\]
\[10x + 13 \geq 0\]
\[10x \geq - 13\ \]
\[x \geq - 1,3.\]
\[M = \left\lbrack - \frac{5}{11};20 \right) \cup (20; + \infty).\]
\[11x + 5 \geq 10x + 13\]
\[x \geq 8.\]
\[Решение\ неравенства:\]
\[x \in \lbrack 8;20) \cup (20; + \infty).\]
\[Ответ:\ x \in \lbrack 8;20) \cup (20; + \infty).\]
\[\textbf{б)}\ \frac{\sqrt{10x + 17}}{|x - 1|} \geq \frac{\sqrt{8x + 11}}{|x - 1|}\]
\[x - 1 \neq 0\]
\[x \neq 1.\]
\[10x + 17 \geq 0\]
\[10x \geq - 17\]
\[x \geq - 1,7.\]
\[8x + 11 \geq 0\]
\[8x \geq - 11\]
\[x \geq - 1,375.\]
\[M = \lbrack - 1,375;1) \cup (1; + \infty).\]
\[10x + 17 \geq 8x + 11\]
\[2x \geq - 6\]
\[x \geq - 3.\]
\[Решение\ неравенства:\]
\[x \in \lbrack - 1,375;1) \cup (1; + \infty).\]
\[Ответ:\ x \in \lbrack - 1,375;1) \cup (1; + \infty).\]
\[\textbf{в)}\ \frac{\sqrt{9x + 19}}{|x + 2|} \leq \frac{\sqrt{11x + 31}}{|x + 2|}\]
\[x + 2 \neq 0\]
\[x \neq - 2.\]
\[9x + 19 \geq 0\]
\[9x \geq - 19\ \]
\[x \geq - 2\frac{1}{9}.\]
\[11x + 31 \geq 0\]
\[11x \geq - 31\]
\[x \geq - 2\frac{9}{11}.\]
\[M = \left\lbrack - 2\frac{1}{9}; - 2 \right) \cup ( - 2; + \infty).\]
\[9x + 19 \leq 11x + 31\]
\[2x \geq - 12\]
\[x \geq - 6.\]
\[Решение\ неравенства:\]
\[x \in \left\lbrack - 2\frac{1}{9}; - 2 \right) \cup ( - 2; + \infty).\]
\[Ответ:\ x \in \left\lbrack - 2\frac{1}{9}; - 2 \right) \cup ( - 2; + \infty).\]
\[\textbf{г)}\ \frac{\sqrt{8x + 21}}{|x + 1|} \leq \frac{\sqrt{10x + 41}}{|x + 1|}\ \]
\[x + 1 \neq 0\]
\[x \neq - 1.\]
\[8x + 21 \geq 0\]
\[8x \geq - 21\]
\[x \geq - 2\frac{5}{8}.\]
\[10x + 41 \geq 0\]
\[10x \geq - 41\]
\[x \geq - 4,1.\]
\[M = \left\lbrack - 2\frac{5}{8}; - 1 \right) \cup ( - 1; + \infty).\]
\[8x + 21 \leq 10x + 41\]
\[2x \geq - 20\]
\[x \geq - 10.\]
\[Решение\ неравенства:\]
\[x \in \left\lbrack - 2\frac{5}{8}; - 1 \right) \cup ( - 1; + \infty).\]
\[Ответ:\ x \in \left\lbrack - 2\frac{5}{8}; - 1 \right) \cup ( - 1; + \infty).\]
\[\boxed{\mathbf{63.}}\]
\[\textbf{а)}\ \sqrt{4\lg x - 24} \geq 9 - \lg x\]
\[1)\ \left\{ \begin{matrix} \sqrt{4\lg x - 24} = 9 - \lg x \\ \sqrt{4\lg x - 24} > 9 - \lg x \\ \end{matrix} \right.\ \]
\[\sqrt{4\lg x - 24} = 9 - \lg x\]
\[4\lg x - 24 = \left( 9 - \lg x \right)^{2}\]
\[4\lg x - 24 = 81 - 18\lg x + lg^{2}x\]
\[lg^{2}x - 22\lg x + 105 = 0\]
\[\lg x = y:\]
\[y^{2} - 22y + 105 = 0\]
\[D = 121 - 105 = 16\]
\[y_{1} = 11 + 4 = 15;\]
\[y_{2} = 11 - 4 = 7;\]
\[\lg{x =}7\]
\[x = 10^{7}.\]
\[\lg x = 15\]
\[x = 10^{15}.\]
\[9 - \lg x \geq 0\]
\[\lg x \leq 9\]
\[0 < x \leq 10^{9}.\]
\[x = 10^{7} - корень\ уравнения.\]
\[2)\ \left\lbrack \begin{matrix} \left\{ \begin{matrix} \left( \sqrt{4\lg x - 24} \right)^{2} > \left( 9 - \lg x \right)^{2} \\ \lg x \geq 9\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \\ \left\{ \begin{matrix} 4\lg x - 24 \geq 0 \\ 9 - \lg x < 0\ \ \ \ \ \ \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } \\ \end{matrix} \right.\ \ \]
\[\left\lbrack \begin{matrix} \left\{ \begin{matrix} x < 10^{7};\ \ \ x > 10^{15} \\ 0 < x \leq 10^{9}\text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ } \\ \end{matrix} \right.\ \\ \left\{ \begin{matrix} x \geq 10^{6} \\ x > 10^{9} \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} 10^{7} < x < 10^{9} \\ x > 10^{9}\text{\ \ \ \ \ \ \ \ \ \ \ \ } \\ \end{matrix} \right.\ \]
\[x \in \left\lbrack 10^{7}; + \infty \right).\]
\[Ответ:x \in \left\lbrack 10^{7}; + \infty \right).\]
\[\textbf{б)}\ \sqrt{9\lg x - 3} \leq 1 - 4\lg x\]
\[1)\ \left\{ \begin{matrix} \sqrt{9\lg x - 3} = 1 - 4\lg x \\ \sqrt{9\lg x - 3} < 1 - 4\lg x \\ \end{matrix} \right.\ \]
\[\sqrt{9\lg x - 3} = 1 - 4\lg x\]
\[9\lg x - 3 = \left( 1 - 4\lg x \right)^{2}\]
\[9\lg x - 3 = 1 - 8\lg x + 16lg^{2}x\]
\[16lg^{2}x - 17\lg x + 4 = 0\]
\[\lg x = y:\]
\[16y^{2} - 17y + 4 = 0\]
\[D = 289 - 256 = 33\]
\[y_{1} = \frac{17 + \sqrt{33}}{32};\]
\[y_{2} = \frac{17 - \sqrt{33}}{32};\]
\[\log x = \frac{17 + \sqrt{33}}{32};\]
\[\log x = \frac{17 - \sqrt{33}}{32}.\]
\[1 - 4\lg x \geq 0\]
\[\lg x \leq \frac{1}{4}.\]
\[2)\ \left\{ \begin{matrix} 16y^{2} - 17y + 4 < 0 \\ 9\log x - 3 \geq 0\ \ \ \ \ \ \ \ \ \ \\ 1 - 4\lg x > 0\ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} x < \frac{17 - \sqrt{33}}{32} \\ x > \frac{17 + \sqrt{33}}{32} \\ \lg x \geq \frac{1}{3}\text{\ \ \ \ \ \ \ \ \ \ \ } \\ \lg x < \frac{1}{4}\text{\ \ \ \ \ \ \ \ \ \ \ } \\ \end{matrix} \right.\ \]
\[Нет\ решений.\]
\[Ответ:нет\ решений.\]
\[\textbf{в)}\ \sqrt{4\lg x - 16} \geq 7 - \lg x\]
\[1)\ \left\{ \begin{matrix} \sqrt{4\lg x - 16} = 7 - \lg x \\ \sqrt{4\lg x - 16} > 7 - \lg x \\ \end{matrix} \right.\ \]
\[\sqrt{4\lg x - 16} = 7 - \lg x\]
\[4\lg x - 16 = \left( 7 - \lg x \right)^{2}\]
\[4\lg x - 16 = 49 - 14\lg x + lg^{2}x\]
\[lg^{2}x - 18\lg x + 65 = 0\]
\[\lg x = y:\]
\[y^{2} - 18y + 65 = 0\]
\[D = 81 - 65 = 16\]
\[y_{1} = 9 + 4 = 13;\]
\[y_{2} = 9 - 4 = 5;\]
\[\lg x = 13\]
\[x = 10^{13}.\]
\[\lg x = 5\]
\[x = 10^{5}.\]
\[7 - \lg x \geq 0\]
\[\lg x \leq 7\]
\[0 < x \leq 10^{7}.\]
\[x = 10^{7} - решение\ уравнения.\]
\[2)\ \left\lbrack \begin{matrix} \left\{ \begin{matrix} lg^{2}x - 18\lg x + 65 > 0 \\ 7 - \lg x \geq 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \\ \left\{ \begin{matrix} 4\lg x - 16 \geq 0 \\ 7 - \lg x < 0\ \ \ \ \ \ \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } \\ \end{matrix} \right.\ \]
\[Первая\ система:\]
\[\left\{ \begin{matrix} x < 10^{5}\text{\ \ } \\ x > 10^{13} \\ x \leq 10^{7}\text{\ \ } \\ \end{matrix} \right.\ \]
\[10^{5} < x \leq 10^{7}.\]
\[Вторая\ система:\]
\[\left\{ \begin{matrix} 4\lg x \geq 16 \\ \lg x > 7\ \ \ \ \ \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} \lg x \geq 4 \\ x > 10^{7} \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} x \geq 10^{4} \\ x > 10^{7} \\ \end{matrix} \right.\ \]
\[x > 10^{7}.\]
\[Общее\ решение\ системы:\]
\[x \in \left\lbrack 10^{5}; + \infty \right).\]
\[Ответ:x \in \left\lbrack 10^{5}; + \infty \right).\]
\[\textbf{г)}\ \sqrt{12\lg x - 8} \leq 1 - 3\lg x\]
\[1)\ \left\{ \begin{matrix} \sqrt{12\lg x - 8} = 1 - 3\lg x \\ \sqrt{12\lg x - 8} < 1 - 3\lg x \\ \end{matrix} \right.\ \]
\[\sqrt{12\lg x - 8} = 1 - 3\lg x\]
\[12\lg x - 8 = \left( 1 - 3\lg x \right)^{2}\]
\[12\lg x - 8 = 1 - 6\lg x + 9lg^{2}x\]
\[9lg^{2}x - 18\lg x + 9 = 0\ \ \ \]
\[9 \cdot (lg^{2}x - 2\lg x + 1) = 0\]
\[9 \cdot \left( \lg x - 1 \right)^{2} = 0\]
\[\lg x - 1 = 0\]
\[\lg x = 1.\]
\[2)\ \left\{ \begin{matrix} \lg x = 1\ \ \ \ \ \ \ \ \ \ \ \\ 1 - 3\lg x \geq 0 \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} \lg x = 1\ \ \\ 3\lg x \leq 1 \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} \lg x = 1\ \\ \lg x \leq \frac{1}{3}. \\ \end{matrix} \right.\ \]
\[3)\ \left\{ \begin{matrix} 9 \cdot \left( \lg x - 1 \right)^{2} < 0 \\ 12\lg x - 8 \geq 0\ \ \ \ \ \ \\ 1 - 3\lg x > 0\ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} \lg x < \frac{1}{2} \\ \lg x \geq \frac{2}{3} \\ \lg x < \frac{1}{3} \\ \end{matrix} \right.\ \]
\[нет\ решений.\]
\[Ответ:нет\ решений.\]
\[\boxed{\mathbf{64.}}\]
\[\textbf{а)}\log_{6x}{(x^{2} - 17x + 60)} \leq 1\]
\[1)\ x^{2} - 17x + 60 > 0\]
\[x_{1} + x_{2} = 17;\ \ x_{1} \cdot x_{2} = 60\]
\[x_{1} = 5;\ \ x_{2} = 12;\]
\[(x - 5)(x - 12) > 0\]
\[x < 5;\ \ x > 12.\]
\[6x > 0\]
\[x > 0.\]
\[6x \neq 1\]
\[x \neq \frac{1}{6}.\]
\[M = \left( 0;\frac{1}{6} \right) \cup \left( \frac{1}{6};5 \right) \cup (12; + \infty).\]
\[2)\ \log_{6x}{(x^{2} - 17x + 60)} = \frac{\lg\left( x^{2} - 17x + 60 \right)}{\lg{6x}}\]
\[\left\{ \begin{matrix} \frac{\lg\left( x^{2} - 17x + 60 \right)}{\lg{6x}} = 1 \\ \frac{\lg\left( x^{2} - 17x + 60 \right)}{\lg{6x}} < 1 \\ \end{matrix} \right.\ \]
\[\lg{(x^{2} - 17x + 60)} = \lg{6x}\]
\[x^{2} - 17x + 60 = 6x\]
\[x^{2} - 23x + 60 = 0\]
\[x_{1} + x_{2} = 23;\ \ x_{1} \cdot x_{2} = 60\]
\[x_{1} = 3;\ \ \ x_{2} = 20.\]
\[M = \left( 0;\frac{1}{6} \right):\]
\[\lg{6x} < 0;\]
\[\frac{\lg\left( x^{2} - 17x + 60 \right)}{\lg{6x}} - 1 < 0\]
\[\lg\left( x^{2} - 17x + 60 \right) - \lg{6x} > 0\]
\[x^{2} - 17x + 60 > 6x\]
\[x^{2} - 23x + 60 > 0\]
\[(x - 3)(x - 20) > 0\]
\[x < 3;\ \ \ x > 20.\]
\[M = \left( \frac{1}{6};5 \right) \cup (12; + \infty):\]
\[\lg{6x} >\]
\[\lg\left( x^{2} - 17x + 60 \right) - \lg{6x} < 0\]
\[x^{2} - 17x + 60 < 6x\]
\[x^{2} - 23x + 60 < 0\]
\[(x - 3)(x - 20) > 0\]
\[3 < x < 20.\]
\[Объединим\ решения:\]
\[x \in \left( 0;\frac{1}{6} \right) \cup \lbrack 3;5) \cup (12;20\rbrack.\]
\[Ответ:x \in \left( 0;\frac{1}{6} \right) \cup \lbrack 3;5) \cup (12;20\rbrack.\]
\[\textbf{б)}\log_{6x}\left( x^{2} - 15x + 54 \right) \geq 1\]
\[1)\ x^{2} - 15x + 54 > 0\]
\[x_{1} + x_{2} = 15;\ \ \ x_{1} \cdot x_{2} = 64\]
\[x_{1} = 6;\ \ x_{2} = 9;\]
\[(x - 6)(x - 9) > 0\]
\[x < 6;\ \ \ x > 9.\]
\[6x > 0\]
\[x > 0.\]
\[6x \neq 1\]
\[x \neq \frac{1}{6}.\]
\[M = \left( 0;\frac{1}{6} \right) \cup \left( \frac{1}{6};6 \right) \cup (9; + \infty).\]
\[2)\ \log_{6x}\left( x^{2} - 15x + 54 \right) = \frac{\lg{(x^{2} - 15x + 54)}}{\lg{6x}}\]
\[\left\{ \begin{matrix} \frac{\lg{(x^{2} - 15x + 54)}}{\lg{6x}} = 1 \\ \frac{\lg{(x^{2} - 15x + 54)}}{\lg{6x}} > 1 \\ \end{matrix} \right.\ \]
\[\lg\left( x^{2} - 15x + 54 \right) = \lg{6x}\]
\[x^{2} - 15x + 54 = 6x\]
\[x^{2} - 21x + 54 = 0\]
\[x_{1} + x_{2} = 21;\ \ x_{1} \cdot x_{2} = 54\]
\[x_{1} = 3;\ \ x_{2} = 18.\]
\[M = \left( 0;\frac{1}{6} \right):\]
\[\lg{6x} < 0;\]
\[\lg{\left( x^{2} - 15x + 54 \right) - \lg{6x}} < 0\]
\[x^{2} - 15x + 54 - 6x < 0\]
\[x^{2} - 21x + 54 < 0\]
\[(x - 3)(x - 18) < 0\]
\[3 < x < 18.\]
\[M = \left( \frac{1}{6};6 \right) \cup (9; + \infty):\]
\[\lg{6x} > 0;\]
\[\frac{\lg\left( x^{2} - 15x + 54 \right)}{\lg{6x}} - 1 > 0\]
\[\lg{\left( x^{2} - 15x + 54 \right) - \lg{6x}} > 0\]
\[x^{2} - 15x + 54 - 6x > 0\]
\[x^{2} - 21x + 54 > 0\]
\[(x - 3)(x - 18) > 0\]
\[x < 3;\ \ \ x > 18.\]
\[Объединим\ решения:\]
\[x \in \left( \frac{1}{6};3 \right\rbrack \cup \lbrack 18; + \infty).\]
\[Ответ:x \in \left( \frac{1}{6};3 \right\rbrack \cup \lbrack 18; + \infty).\]
\[\textbf{в)}\log_{12x}{(x^{2} - 19x + 84)} \leq 1\]
\[1)\ x^{2} - 19x + 84 > 0\]
\[x_{1} + x_{2} = 19;\ \ x_{1} \cdot x_{2} = 84\]
\[x_{1} = 7;\ \ x_{2} = 12;\]
\[(x - 7)(x - 12) > 0\]
\[x < 7;\ \ x > 12.\]
\[12x > 0\]
\[x > 0.\]
\[12x \neq 0\]
\[x \neq \frac{1}{12}.\]
\[M = \left( 0;\frac{1}{12} \right) \cup \left( \frac{1}{12};7 \right) \cup (12; + \infty).\]
\[2)\ \log_{12x}{(x^{2} - 19x + 84)} = \frac{\lg\left( x^{2} - 19x + 84 \right)}{\lg{12x}}\]
\[\left\{ \begin{matrix} \frac{\lg\left( x^{2} - 19x + 84 \right)}{\lg{12x}} = 1 \\ \frac{\lg\left( x^{2} - 19x + 84 \right)}{\lg{12x}} < 1 \\ \end{matrix} \right.\ \]
\[\lg\left( x^{2} - 19x + 84 \right) = \lg{12x}\]
\[x^{2} - 19x + 84 = 12x\]
\[x^{2} - 31x + 84 = 0\]
\[x_{1} + x_{2} = 31;\ \ x_{1} \cdot x_{2} = 84\]
\[x_{1} = 3;\ \ \ x_{2} = 28.\]
\[M = \left( 0;\frac{1}{12} \right):\]
\[\lg{12x} < 0;\]
\[\frac{\lg\left( x^{2} - 19x + 84 \right)}{\lg{12x}} - 1 < 0\]
\[\lg\left( x^{2} - 19x + 84 \right) - \lg{12x} > 0\]
\[x^{2} - 19x + 84 - 12x > 0\]
\[x^{2} - 31x + 84 > 0\]
\[(x - 3)(x - 28) > 0\]
\[x < 3;\ \ x > 28.\]
\[M = \left( \frac{1}{12};7 \right) \cup (12; + \infty):\]
\[\lg{12x} > 0;\]
\[\lg\left( x^{2} - 19x + 84 \right) - \lg{12x} < 0\]
\[x^{2} - 19x + 84 - 12x < 0\]
\[x^{2} - 31x + 84 < 0\]
\[(x - 3)(x - 28) < 0\]
\[3 < x < 28.\]
\[Объединим\ решения:\]
\[x \in \left( 0;\frac{1}{12} \right) \cup \lbrack 3;7) \cup (12;28\rbrack.\]
\[Ответ:x \in \left( 0;\frac{1}{12} \right) \cup \lbrack 3;7) \cup (12;28\rbrack.\]
\[\textbf{г)}\log_{7x}\left( x^{2} - 16x + 60 \right) \geq 1\]
\[1)\ x^{2} - 16x + 60 > 0\]
\[D_{1} = 64 - 60 = 4\]
\[x_{1} = 8 + 2 = 10;\]
\[x_{2} = 8 - 2 = 6;\]
\[(x - 6)(x - 10) > 0\]
\[x < 6;\ \ x > 10.\]
\[7x > 0\]
\[x > 0.\]
\[7x \neq 1\]
\[x \neq \frac{1}{7}.\]
\[M = \left( 0;\frac{1}{7} \right) \cup \left( \frac{1}{7};6 \right) \cup (10; + \infty).\]
\[2)\ \log_{7x}\left( x^{2} - 16x + 60 \right) = \frac{\lg\left( x^{2} - 16x + 60 \right)}{\lg{7x}}\]
\[\left\{ \begin{matrix} \frac{\lg\left( x^{2} - 16x + 60 \right)}{\lg{7x}} = 1 \\ \frac{\lg\left( x^{2} - 16x + 60 \right)}{\lg{7x}} > 1 \\ \end{matrix} \right.\ \]
\[\lg\left( x^{2} - 16x + 60 \right) = \lg{7x}\]
\[x^{2} - 16x + 60 = 7x\]
\[x^{2} - 23x + 60 = 0\]
\[x_{1} + x_{2} = 23;\ \ x_{1} \cdot x_{2} = 60\]
\[x_{1} = 3;\ \ \ x_{2} = 20.\]
\[M = \left( 0;\frac{1}{7} \right):\]
\[\lg{7x} < 0;\]
\[\lg\left( x^{2} - 16x + 60 \right) < \lg{7x}\]
\[x^{2} - 16x + 60 < 7x\]
\[x^{2} - 23x + 60 < 0\]
\[(x - 3)(x - 20) < 0\]
\[3 < x < 20.\]
\[M = \left( \frac{1}{7};6 \right) \cup (10; + \infty):\]
\[\lg{7x} > 0;\]
\[\lg\left( x^{2} - 16x + 60 \right) > \lg{7x}\]
\[x^{2} - 16x + 60 > 7x\]
\[x^{2} - 23x + 60 > 0\]
\[(x - 3)(x - 20) > 0\]
\[x < 3;\ \ \ x > 20.\]
\[Объединим\ решения:\]
\[x \in \left( \frac{1}{7};3 \right\rbrack \cup \lbrack 20;\ + \infty).\]
\(Ответ:x \in \left( \frac{1}{7};3 \right\rbrack \cup \lbrack 20;\ + \infty).\)
## Параграф 12. Метод промежутков для уравнений и неравенств
\[\boxed{\mathbf{1.}}\]
\[\textbf{а)}\ |x - 1| = 2x + 4\]
\[x - 1 = 0\]
\[x = 1.\]
\[x < 1:\]
\[- x + 1 = 2x + 4\]
\[3x = - 3\]
\[x = - 1.\]
\[x \geq 1:\]
\[x - 1 = 2x + 4\]
\[x = - 5\]
\[нет\ корней.\]
\[Ответ:x = - 1.\]
\[\textbf{б)}\ |x - 2| = 2x + 1\]
\[x - 2 = 0\]
\[x = 2.\]
\[x < 2:\]
\[- x + 2 = 2x + 1\]
\[3x = 1\]
\[x = \frac{1}{3}.\]
\[x \geq 2:\]
\[x - 2 = 2x + 1\]
\[x = - 3\]
\[нет\ корней.\]
\[Ответ:x = \frac{1}{3}.\]
\[\textbf{в)}\ |x - 1| + |x + 1| = 4\]
\[x - 1 = 0\]
\[x = 1.\]
\[x + 1 = 0\]
\[x = - 1.\]
\[x < - 1:\]
\[1 - x - 1 - x = 4\]
\[- 2x = 4\]
\[x = - 2.\]
\[- 1 \leq x < 1:\]
\[1 - x + 1 + x = 4\]
\[0x = 2\]
\[нет\ корней.\]
\[x \geq 1:\]
\[x - 1 + x + 1 = 4\]
\[2x = 4\]
\[x = 2.\]
\[Ответ:x = \pm 2.\]
\[\textbf{г)}\ |x - 3| + |x + 3| = 8\]
\[x - 3 = 0\]
\[x = 3.\]
\[x + 3 = 0\]
\[x = - 3.\]
\[x < - 3:\]
\[3 - x - 3 - x = 8\]
\[- 2x = 8\]
\[x = - 4.\]
\[- 3 \leq x < 3:\]
\[3 - x + 3 + x = 8\]
\[0x = 2\]
\[нет\ корней.\]
\[x \geq 3:\]
\[x - 3 + x + 3 = 8\]
\[2x = 8\]
\[x = 4.\]
\[Ответ:x = \pm 4.\]
\[\textbf{д)}\ |x - 1| + |x - 2| + |x - 3| = 2\]
\[x = 1;\ \ x = 2;\ \ x = 3.\]
\[x < 1:\]
\[1 - x + 2 - x + 3 - x = 2\]
\[- 3x + 6 = 2\]
\[- 3x = - 4\]
\[x = \frac{4}{3} = 1\frac{1}{3}\]
\[нет\ корней.\]
\[1 \leq x < 2:\]
\[x - 1 + 2 - x + 3 - x = 2\]
\[- x + 4 = 2\]
\[- x = - 2\]
\[x = 2.\]
\[нет\ корней.\]
\[2 \leq x < 3:\]
\[x - 1 + x - 2 + 3 - x = 2\]
\[x = 2.\]
\[x \geq 3:\]
\[x - 1 + x - 2 + x - 3 = 2\]
\[3x = 2 + 6\]
\[3x = 8\]
\[x = \frac{8}{3} = 2\frac{2}{3}.\]
\[нет\ корней.\]
\[Ответ:x = 2.\]
\[\textbf{е)}\ |x + 1| + |x - 3| + |x - 5| = 7\]
\[x = - 1;\ \ x = 3;\ \ x = 5.\]
\[x < - 1:\]
\[- x - 1 + 3 - x + 5 - x = 7\]
\[- 3x = 7 - 7\]
\[x = 0.\]
\[нет\ корней.\]
\[- 1 \leq x < 3:\]
\[x + 1 + 3 - x + 5 - x = 7\]
\[- x = 7 - 9\]
\[- x = - 2\]
\[x = 2.\]
\[3 \leq x < 5:\]
\[x + 1 + x - 3 + 5 - x = 7\]
\[x = 7 - 3\]
\[x = 4.\]
\[x \geq 5:\]
\[x + 1 + x - 3 + x - 5 = 7\]
\[3x = 7 + 7\]
\[3x = 14\]
\[x = \frac{14}{3} = 4\frac{2}{3}.\]
\[нет\ корней.\]
\[Ответ:x = 2;\ \ x = 4.\]
\[\boxed{\mathbf{2.}}\]
\[\textbf{а)}\ |x - 1| = x^{2} - 5x + 4\]
\[x - 1 = 0\]
\[x = 1.\]
\[x < 1:\]
\[- x + 1 = x^{2} - 5x + 4\]
\[x^{2} - 4x + 3 = 0\]
\[D_{1} = 4 - 3 = 1\]
\[x_{1} = 2 + 1 = 3;\]
\[x_{2} = 2 - 1 = 1.\]
\[нет\ корней.\]
\[x \geq 1:\]
\[x - 1 = x^{2} - 5x + 4\]
\[x^{2} - 6x + 5 = 0\]
\[D_{1} = 9 - 5 = 4\]
\[x_{1} = 3 + 2 = 5;\]
\[x_{2} = 3 - 2 = 1.\]
\[Ответ:x = 1;x = 5.\]
\[\textbf{б)}\ |x - 2| = x^{2} - 4x - 2\]
\[x - 2 = 0\]
\[x = 2.\]
\[x < 2:\]
\[- x + 2 = x^{2} - 4x - 2\]
\[x^{2} - 3x - 4 = 0\]
\[x_{1} + x_{2} = 3;\ \ x_{1} \cdot x_{2} = - 4\]
\[x_{1} = - 1;\ \ \]
\[x_{2} = 4\ (не\ принадлежит\ промежутку).\]
\[x \geq 2:\]
\[x - 2 = x^{2} - 4x - 2\]
\[x^{2} - 5x = 0\]
\[x(x - 5) = 0\]
\[x = 0\ (не\ принадлежит\ промежутку).\]
\[x = 5.\]
\[Ответ:x = - 1;\ \ x = 5.\]
\[\textbf{в)}\ |x - 3| = x^{2} - 6x + 3\]
\[x - 3 = 0\]
\[x = 3.\]
\[x < 3:\]
\[- x + 3 = x^{2} - 6x + 3\]
\[x^{2} - 5x = 0\]
\[x(x - 5) = 0\]
\[x = 0;\]
\[x = 5\ (не\ принадлежит\ промежутку).\]
\[x \geq 3:\]
\[x - 3 = x^{2} - 6x + 3\]
\[x^{2} - 7x + 6 = 0\]
\[x_{1} + x_{2} = 7;\ \ \ x_{1} \cdot x_{2} = 6\]
\[x_{1} = 1\ (не\ принадлежит\ промежутку);\]
\[x_{2} = 6.\]
\[Ответ:x = 0;x = 6.\]
\[\textbf{г)}\ |x - 4| = x^{2} - 2x - 2\]
\[x - 4 = 0\]
\[x = 4.\]
\[x < 4:\]
\[- x + 4 = x^{2} - 2x - 2\]
\[x^{2} - x - 6 = 0\]
\[x_{1} + x_{2} = 1;\ \ x_{1} \cdot x_{2} = - 6\]
\[x_{1} = 3;\ \ \ x_{2} = - 2.\]
\[x \geq 4:\]
\[x - 4 = x^{2} - 2x - 2\]
\[x^{2} - 3x + 2 = 0\]
\[x_{1} + x_{2} = 3;\ \ x_{1} \cdot x_{2} = 2\]
\[x_{1} = 1\ (не\ принадлежит\ промежутку);\]
\[x_{2} = 2\ (не\ принадлежит\ промежутку).\]
\[Ответ:x = - 2;x = 3.\]
\[\boxed{\mathbf{3.}}\]
\[\textbf{а)}\ \left| x^{2} + 4x + 2 \right| = x + 2\]
\[x^{2} + 4x + 2 = 0\]
\[D_{1} = 4 - 2 = 2\]
\[x_{1} = - 2 + \sqrt{2};\]
\[x_{2} = - 2 - \sqrt{2}.\]
\[x < - 2 - \sqrt{2};\ \ x > - 2 + \sqrt{2}:\]
\[x^{2} + 4x + 2 = x + 2\]
\[x^{2} + 3x = 0\]
\[x(x + 3) = 0\]
\[x = 0;\ \ \]
\[x = - 3\ (не\ принадлежит\ промежутку).\]
\[- 2 - \sqrt{2} \leq x \leq - 2 + \sqrt{2}:\]
\[- x^{2} - 4x - 2 = x + 2\]
\[x^{2} + 5x + 4 = 0\]
\[x_{1} + x_{2} = - 5;\ \ \ x_{1} \cdot x_{2} = 4\]
\[x_{1} = - 1;\ \ \]
\[x_{2} = - 4\ (не\ принадлежит\ промежутку).\]
\[Ответ:x = - 1;\ \ x = 0.\]
\[\textbf{б)}\ \left| x^{2} + 6x + 7 \right| = - x - 3\]
\[x^{2} + 6x + 7 = 0\]
\[D_{1} = 9 - 7 = 2\]
\[x_{1} = - 3 - \sqrt{2};\]
\[x_{2} = - 3 + \sqrt{2}.\]
\[x < - 3 - \sqrt{2};\ x > - 3 + \sqrt{2}:\]
\[x^{2} + 6x + 7 = - x - 3\]
\[x^{2} + 7x + 10 = 0\]
\[x_{1} + x_{2} = - 7;\ \ \]
\[x_{1} \cdot x_{2} = 10\]
\[x_{1} = - 5\ (не\ принадлежит\ промежутку);\ \ \]
\[x_{2} = - 2.\]
\[- 3 - \sqrt{2} \leq x \leq - 3 + \sqrt{2}:\]
\[- x^{2} - 6x - 7 = - x - 3\]
\[x^{2} + 5x + 4 = 0\]
\[x_{1} + x_{2} = - 5;\ \ x_{1} \cdot x_{2} = 4\]
\[x_{1} = - 4;\]
\[x_{2} = - 1\ (не\ принадлежит\ промежутку).\]
\[Ответ:x = - 4;\ \ x = - 2.\]
\[\textbf{в)}\ \left| x^{2} - 2x - 2 \right| = - x + 4\]
\[x^{2} - 2x - 2 = 0\]
\[D_{1} = 1 + 2 = \sqrt{3}\]
\[x_{1} = 1 + \sqrt{3};\]
\[x_{2} = 1 - \sqrt{3}.\]
\[x < 1 - \sqrt{3};\ \ x > 1 + \sqrt{3}:\]
\[x^{2} - 2x - 2 = - x + 4\]
\[x^{2} - x - 6 = 0\]
\[x_{1} + x_{2} = 1;\ \ x_{1} \cdot x_{2} = - 6\]
\[x_{1} = - 2\ (не\ принадлежит\ промежутку);\ \ \]
\[x_{2} = 3\ (не\ принадлежит\ промежутку).\]
\[1 - \sqrt{3} \leq x \leq 1 + \sqrt{3}:\]
\[- x^{2} + 2x + 2 = - x + 4\]
\[x^{2} - 3x + 2 = 0\]
\[x_{1} + x_{2} = 3;\ \ x_{1} \cdot x_{2} = 2\]
\[x_{1} = 1;\ \ \ x_{2} = 2.\]
\[Ответ:x = 1;x = 2.\]
\[\textbf{г)}\ \left| x^{2} - 4x + 1 \right| = x + 1\]
\[x^{2} - 4x + 1 = 0\]
\[D_{1} = 4 - 1 = 3\]
\[x_{1} = 2 + \sqrt{3};\]
\[x_{2} = 2 - \sqrt{3}.\]
\[x < 2 - \sqrt{3};\ \ x > 2 + \sqrt{3}:\]
\[x^{2} - 4x + 1 = x + 1\]
\[x^{2} - 5x = 0\]
\[x(x - 5) = 0\]
\[x_{1} = 0;\ \ x_{2} = 5.\]
\[2 - \sqrt{3} \leq x \leq 2 + \sqrt{3}:\]
\[- x^{2} + 4x - 1 = x + 1\]
\[x^{2} - 3x + 2 = 0\]
\[x_{2} + x_{2} = 3;\ \ \ x_{1} \cdot x_{2} = 2\]
\[x_{1} = 1\ (не\ принадлежит\ промежутку);\]
\[x_{2} = 2\ (не\ принадлежит\ промежутку).\]
\[Ответ:x = 0;\ \ x = 5.\]
\[\boxed{\mathbf{4.}}\]
\[\textbf{а)}\ \left| x^{2} - x - 1 \right| = x^{2} + 2x + 1\]
\[x^{2} - x - 1 = 0\]
\[D = 1 + 4 = 5\]
\[x_{1} = \frac{1 + \sqrt{5}}{2};\]
\[x_{2} = \frac{1 - \sqrt{5}}{2}.\]
\[x < \frac{1 - \sqrt{5}}{2};x > \frac{1 + \sqrt{5}}{2}:\]
\[x^{2} - x - 1 = x^{2} + 2x + 1\]
\[- 3x = 2\]
\[x = - \frac{2}{3}.\]
\[\frac{1 - \sqrt{5}}{2} \leq x \leq \frac{1 + \sqrt{5}}{2}:\]
\[- x^{2} + x + 1 = x^{2} + 2x + 1\]
\[2x^{2} + x = 0\]
\[2x\left( x + \frac{1}{2} \right) = 0\]
\[x = 0;\ \ x = - 0,5.\]
\[Ответ:x = - \frac{2}{3};x = - 0,5;\ x = 0.\]
\[\textbf{б)}\ \left| x^{2} - 2x - 2 \right| = x^{2} - 4x + 6\]
\[x^{2} - 2x - 2 = 0\]
\[D_{1} = 1 + 2 = 3\]
\[x_{1} = 1 + \sqrt{3};\]
\[x_{2} = 1 - \sqrt{3}.\]
\[x < 1 - \sqrt{3};\ \ x > 1 + \sqrt{3}:\]
\[x^{2} - 2x - 2 = x^{2} - 4x + 6\]
\[- 2x = - 8\]
\[x = 4.\]
\[1 - \sqrt{3} \leq x \leq 1 + \sqrt{3}:\]
\[- x^{2} + 2x + 2 = x^{2} - 4x + 6\]
\[2x^{2} - 6x + 4 = 0\ \ \ \ |\ :2\]
\[x^{2} - 3x + 2 = 0\]
\[x_{1} + x_{2} = 3;\ \ \ x_{1} \cdot x_{2} = 2\]
\[x_{1} = 1;\ \ \ x_{2} = 2.\]
\[Ответ:x = 1;x = 2;x = 4.\]
\[\textbf{в)}\ \left| x^{2} - 2x - 4 \right| = x^{2} - 4x + 4\]
\[x^{2} - 2x - 4 = 0\]
\[D_{1} = 1 + 4 = 5\]
\[x_{1} = 1 + \sqrt{5};\]
\[x_{2} = 1 - \sqrt{5}.\]
\[x < 1 - \sqrt{5};\ \ x > 1 + \sqrt{5}:\]
\[x^{2} - 2x - 4 = x^{2} - 4x + 4\]
\[2x = 8\]
\[x = 4.\]
\[1 - \sqrt{5} \leq x \leq 1 + \sqrt{5}:\]
\[- x^{2} + 2x + 4 = x^{2} - 4x + 4\]
\[2x^{2} - 6x = 0\]
\[2x(x - 3) = 0\]
\[x = 0;\ \ x = 3.\]
\[Ответ:x = 0;x = 3;x = 4.\]
\[\textbf{г)}\ \left| x^{2} - 4x + 2 \right| = x^{2} - 6x + 10\]
\[x^{2} - 4x + 2 = 0\]
\[D_{1} = 4 - 2 = 2\]
\[x_{1} = 2 + \sqrt{2};\]
\[x_{2} = 2 - \sqrt{2}.\]
\[x < 2 - \sqrt{2};x > 2 + \sqrt{2}:\]
\[x^{2} - 4x + 2 = x^{2} - 6x + 10\]
\[- 2x = - 8\]
\[x = 4.\]
\[2 - \sqrt{2} \leq x \leq 2 + \sqrt{2}:\]
\[- x^{2} + 4x - 2 = x^{2} - 6x + 10\]
\[2x^{2} - 10x + 12 = 0\ \ \ |\ :2\]
\[x^{2} - 5x + 6 = 0\]
\[x_{1} + x_{2} = 5;\ \ x_{1} \cdot x_{2} = 6\]
\[x_{1} = 2;\ \ x_{2} = 3.\]
\[Ответ:x = 2;x = 3;x = 4.\]
\[\boxed{\mathbf{5.}}\]
\[\textbf{а)}\ \frac{|2x - 4| + |x - 5|}{|x - 1| + x - 1} = 1\]
\[|x - 1| + x - 1 \neq 0\]
\[|x - 1| \neq - (x - 1)\]
\[x - 1 > 0\]
\[x > 1.\]
\[|2x - 4| + |x - 5| = 0\]
\[x = 2;\ \ x = 5.\]

\[1 < x < 2:\]
\[\frac{- 2x + 4 - x + 5}{x - 1 + x - 1} = 1\]
\[\frac{- 3x + 9}{2x - 2} = 1\]
\[- 3x + 9 = 2x - 2\]
\[5x - 11 = 0\]
\[x = \frac{11}{5} = 2\frac{1}{5}.\]
\[Нет\ корней.\]
\[2 \leq x < 5:\]
\[\frac{2x - 4 - x + 5}{x - 1 + x - 1} = 1\]
\[x + 1 = 2x - 2\]
\[x - 3 = 0\]
\[x = 3.\]
\[x \geq 5:\]
\[\frac{2x - 4 + x - 5}{x - 1 + x - 1} = 1\]
\[\frac{3x - 9}{2x - 2} = 1\]
\[3x - 9 = 2x - 2\]
\[x = 7.\]
\[Ответ:x = 3;\ \ x = 7.\]
\[\textbf{б)}\ \frac{|2x - 1| - |x - 5|}{|x + 1| - x - 1} = - 1\]
\[|x + 1| - x - 1 \neq 0\]
\[|x + 1| \neq x + 1\]
\[x + 1 < 0\]
\[x < - 1.\]
\[|2x - 1| - |x - 5| = 0\]
\[x = 0,5;\ \ x = 5.\]

\[x < - 1:\]
\[\frac{- 2x + 1 + x - 5}{- x - 1 - x - 1} = - 1\]
\[\frac{- x - 4}{- 2x - 2} = - 1\]
\[- x - 4 = 22\]
\[3x = - 6\]
\[x = - 2.\]
\[Ответ:x = - 2.\]
\[\textbf{в)}\ \frac{|2x - 5| + |x + 2|}{|x - 3| + x - 3} = - 0,5\]
\[|x - 3| + x - 3 \neq 0\]
\[|x - 3| \neq - x + 3\]
\[x - 3 > 0\]
\[x > 3.\]
\[|2x - 5| + |x + 2| = 0\]
\[x = 2,5;\ \ x = - 2.\]

\[x > 3:\]
\[\frac{2x - 5 + x + 2}{x - 3 + x - 3} = - 0,5\]
\[\frac{3x - 3}{2x - 6} = - 0,5\]
\[3x - 3 = - 0,5(2x - 6)\]
\[3x - 3 = - x + 3\]
\[4x = 6\]
\[x = 1,5.\]
\[Нет\ корней.\]
\[Ответ:нет\ корней.\]
\[\textbf{г)}\ \frac{|2x - 3| - |x + 3|}{|x - 4| - x + 4} = - 1\]
\[|x - 4| - x + 4 \neq 0\]
\[|x - 4| \neq x - 4\]
\[x - 4 < 0\]
\[x < 4.\]
\[|2x - 3| - |x + 3| = 0\]
\[x = 1,5;\ \ x = - 3.\]

\[x < - 3:\]
\[\frac{- 2x + 3 + x + 3}{- x + 4 - x + 4} = - 1\]
\[\frac{- x + 6}{- 2x + 8} = - 1\]
\[- x + 6 = 2x - 8\]
\[3x = 14\]
\[x = \frac{14}{3} = 4\frac{2}{3}.\]
\[Нет\ корней.\]
\[- 3 \leq x < 1,5:\]
\[\frac{- 2x + 3 - x - 3}{- x + 4 - x + 4} = - 1\]
\[\frac{- 3x}{- 2x + 8} = - 1\]
\[- 3x = 2x - 8\]
\[5x = 8\]
\[x = \frac{8}{5} = 1,6.\]
\[Нет\ корней.\]
\[1,5 \leq x < 4:\]
\[\frac{2x - 3 - x - 3}{- x + 4 - x + 4} = - 1\]
\[\frac{x - 6}{- 2x + 8} = - 1\]
\[x - 6 = 2x - 8\]
\[x = 2.\]
\[Ответ:x = 2.\]
\[\boxed{\mathbf{6.}}\]
\[\textbf{а)}\ \frac{|x + 1|}{x + 1} + \frac{|x + 3|}{x + 3} = 0\]
\[x \neq - 3;\ \ x \neq - 1.\]
\[x < - 3:\]
\[- \frac{x + 1}{x + 1} - \frac{x + 3}{x + 3} = 0\]
\[- 2 = 0\]
\[нет\ корней.\]
\[- 3 < x < - 1:\]
\[- \frac{x + 1}{x + 1} + \frac{x + 3}{x + 3} = 0\]
\[- 1 + 1 = 0\]
\[0 = 0.\]
\[- 3 < x < - 1.\]
\[x > - 1:\]
\[\frac{x + 1}{x + 1} + \frac{x + 3}{x + 3} = 0\]
\[1 + 1 = 0\]
\[2 = 0\]
\[нет\ корней.\]
\[Ответ:x \in ( - 3; - 1).\]
\[\textbf{б)}\ \frac{|x - 1|}{x - 1} + \frac{|x + 4|}{x + 4} = - 2\]
\[x \neq 1;\ \ x \neq - 4.\]
\[x < - 4:\]
\[- \frac{x - 1}{x - 1} - \frac{x + 4}{x + 4} = - 2\]
\[- 1 - 1 = - 2\]
\[- 2 = - 2.\]
\[x < - 4.\]
\[- 4 < x < 1:\]
\[- \frac{x - 1}{x - 1} + \frac{x + 4}{x + 4} = - 2\]
\[- 1 + 1 = - 2\]
\[0 = - 2.\]
\[Нет\ корней.\]
\[x > 1:\]
\[\frac{x - 1}{x - 1} + \frac{x + 4}{x + 4} = - 2\]
\[1 + 1 = - 2\]
\[2 = - 2\]
\[нет\ корней.\]
\[Ответ:x \in ( - \infty;4).\]
\[\textbf{в)}\ \frac{|x - 3| - |x - 2|}{|x + 1| + x + 1} = 0\]
\[|x + 1| + x + 1 \neq 0\]
\[|x + 1| \neq - (x + 1)\]
\[x + 1 > 0\]
\[x > - 1.\]
\[|x - 3| - |x - 2| = 0\]
\[x = 3;\ \ x = 2.\]

\[- 1 < x < 2:\]
\[\frac{- x + 3 + x - 2}{x + 1 + x + 1} = 0\]
\[- x + 3 + x - 2 = 0\]
\[1 = 0\]
\[нет\ корней.\]
\[2 \leq x < 3:\]
\[\frac{- x + 3 - x + 2}{x + 1 + x + 1} = 0\]
\[- 2x + 5 = 0\]
\[- 2x = - 5\]
\[x = 2,5.\]
\[x \geq 3:\]
\[\frac{x - 3 - x + 2}{x + 1 + x + 1} = 0\]
\[x - 3 - x + 2 = 0\]
\[- 1 = 0\]
\[нет\ корней.\]
\[Ответ:x = 2,5.\]
\[\textbf{г)}\ \frac{|x - 3| - |x - 2|}{x - 4 - |x - 4|} = 0\]
\[x - 4 - |x - 4| \neq 0\]
\[|x - 4| \neq x - 4\]
\[x - 4 < 0\]
\[x < 4.\]
\[|x - 3| - |x - 2| = 0\]
\[x = 3;\ \ x = 2.\]

\[x < 2:\]
\[\frac{- x + 3 + x - 2}{x - 4 + x - 4} = 0\]
\[- x + 3 + x - 2 = 0\]
\[1 = 0\]
\[нет\ корней.\]
\[2 \leq x < 3:\]
\[\frac{- x + 3 - x + 2}{x - 4 + x - 4} = 0\]
\[- 2x + 5 = 0\]
\[- 2x = - 5\]
\[x = 2,5.\]
\[3 \leq x < 4:\]
\[\frac{x - 3 - x + 2}{x - 4 + x - 4} = 0\]
\[x - 3 - x + 2 = 0\]
\[- 1 = 0\]
\[нет\ корней.\]
\[Ответ:x = 2,5.\]
\[\boxed{\mathbf{7.}}\]
\[\textbf{а)}\ \left| 9 - 3^{x} \right| + |x - 6| = 3^{x} - x + 9\]
\[1)\ 9 - 3^{x} = 0\]
\[3^{2} - 3^{x} = 0\]
\[3^{x} = 3^{2}\]
\[x = 2.\]
\[2)\ x - 6 = 0\]
\[x = 6.\]
\[x < 2:\]
\[9 - 3^{x} - x + 6 = 3^{x} - x + 9\]
\[2 \cdot 3^{x} = 6\]
\[x = 1.\]
\[2 \leq x \leq 6:\]
\[- 9 + 3^{x} - x + 6 = 3^{x} - x + 9\]
\[- 3 = 9\]
\[нет\ корней.\]
\[x > 6:\]
\[- 9 + 3^{x} + x - 6 = 3^{x} - x + 9\]
\[2x = 24\]
\[x = 12.\]
\[Ответ:x = 1;\ \ x = 12.\]
\[\textbf{б)}\ \left| 27 - 3^{x} \right| + |x - 5| = 3^{x} - x + 14\]
\[1)\ 27 - 3^{x} = 0\]
\[3^{3} - 3^{x} = 0\]
\[3^{x} = 3^{3}\]
\[x = 3.\]
\[2)\ x - 5 = 0\]
\[x = 5.\]
\[x \leq 3:\]
\[27 - 3^{x} - x + 5 = 3^{x} - x + 14\]
\[2 \cdot 3^{x} = 18\]
\[3^{x} = 9\]
\[x = 2.\]
\[3 < x \leq 5:\]
\[- 27 - 3^{x} - x + 5 = 3^{x} - x + 14\]
\[- 22 = 14\]
\[нет\ корней.\]
\[x > 5:\]
\[- 27 + 3^{x} + x - 5 = 3^{x} - x + 14\]
\[2x = 46\]
\[x = 23.\]
\[Ответ:x = 2;\ \ x = 23.\]
\[\boxed{\mathbf{8.}}\]
\[\left| f(x) \right| + \left| g(x) \right| = f(x) + g(x)\]




\[Все\ решения\ уравнения\ \left| f(x) \right| + \left| g(x) \right| = f(x) + g(x)\ являются\ \]
\[решениями\ системы.\]
\[Предположим\ обратное.\]





\[\boxed{\mathbf{9.}}\]
\[\textbf{а)}\ \left| \sin x - \frac{1}{2} \right| + \left| \cos x - \frac{\sqrt{3}}{2} \right| = \sin x + \cos x - \frac{1 + \sqrt{3}}{2}\]
\[\left\{ \begin{matrix} \sin x - \frac{1}{2} \geq 0\ \ \ \\ \cos x - \frac{\sqrt{3}}{2} \geq 0 \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} \sin x \geq \frac{1}{2}\text{\ \ \ } \\ \cos x \geq \frac{\sqrt{3}}{2} \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} \frac{\pi}{2} + 2\pi n \leq x \leq \frac{5\pi}{6} + 2\pi n\ \\ - \frac{\pi}{6} + 2\pi k \leq x \leq \frac{\pi}{6} + 2\pi k \\ \end{matrix} \right.\ \]
\[x = \frac{\pi}{6} + 2\pi k;k \in Z.\]
\[Ответ:x = \frac{\pi}{6} + 2\pi k;k \in Z.\]
\[\textbf{б)}\ \left| \sin x - \frac{1}{2} \right| + \left| \sin x - \frac{\sqrt{3}}{2} \right| = \frac{\sqrt{3} - 1}{2}\]
\[\left\{ \begin{matrix} \sin x - \frac{1}{2} \geq 0\ \ \ \\ \frac{\sqrt{3}}{2} - \sin x \geq 0 \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} \sin x \geq \frac{1}{2}\text{\ \ \ } \\ \sin x \leq \frac{\sqrt{3}}{2} \\ \end{matrix}\ \right.\ \]
\[\left\{ \begin{matrix} \frac{\pi}{6} + 2\pi n \leq x \leq \frac{5\pi}{6} + 2\pi n\ \ \ \ \\ - \frac{5\pi}{3} + 2\pi k \leq x \leq \frac{\pi}{3} + 2\pi k \\ \end{matrix} \right.\ \]
\[x \in \left\lbrack \frac{\pi}{6} + 2\pi k;\frac{\pi}{3} + 2\pi k \right\rbrack \cup \left\lbrack - \frac{2\pi}{3} + 2\pi n;\frac{5\pi}{6} + 2\pi n \right\rbrack.\]
\[Ответ:\ \in \left\lbrack \frac{\pi}{6} + 2\pi k;\frac{\pi}{3} + 2\pi k \right\rbrack \cup \left\lbrack - \frac{2\pi}{3} + 2\pi n;\frac{5\pi}{6} + 2\pi n \right\rbrack.\]
\[\textbf{в)}\ \left| 2^{x} - 4 \right| + \left| 4 - \sqrt{x} \right| = 2^{x} - \sqrt{x}\]
\[\left\{ \begin{matrix} 2^{x} - 4 \geq 0 \\ 4 - \sqrt{x} \geq 0 \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} 2^{x} \geq 2^{2} \\ \sqrt{x} \leq 4 \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} x \geq 2\ \ \ \ \ \ \ \ \ \ \ \\ 0 \leq x \leq 16 \\ \end{matrix} \right.\ \]
\[2 \leq x \leq 16.\]
\[Ответ:x \in \lbrack 2;16\rbrack.\]
\[\textbf{г)}\ \left| \log_{3}x - 2 \right| + \left| x^{2} - 11x + 18 \right| = \log_{3}x - x^{2} + 11x - 20\]
\[\left\{ \begin{matrix} \log_{3}x - 2 \geq 0\ \ \ \ \ \ \ \ \ \ \ \ \\ - x^{2} + 11x - 18 \geq 0 \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} \log_{3}x \geq 2\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ x^{2} - 11x + 18 \leq 0 \\ \end{matrix} \right.\ \]
\[\log_{3}x \geq 2\]
\[x \geq 3^{2}\]
\[x \geq 9.\]
\[x^{2} - 11x + 18 \leq 0\]
\[x_{1} + x_{2} = 11;\ \ x_{1} \cdot x_{2} = 18\]
\[x_{1} = 2;\ \ x_{2} = 9;\]
\[(x - 2)(x - 9) \leq 0\]
\[2 \leq x \leq 9.\]
\[x \in \lbrack 2;9\rbrack.\]
\[Ответ:\ x \in \lbrack 2;9\rbrack.\]
\[\boxed{\mathbf{10.}}\]
\[\textbf{а)}\ |3x - 6| > x + 2\]
\[3x - 6 = 0\]
\[3x = 6\]
\[x = 2.\]
\[x \leq 2:\]
\[- 3x + 6 > x + 2\]
\[- 4x > - 4\]
\[x < 1.\]
\[x > 2:\]
\[3x - 6 > x + 2\]
\[2x > 8\]
\[x > 4.\]
\[Объединим\ решения:\]
\[x \in ( - \infty;1) \cup (4; + \infty).\]
\[Ответ:x \in ( - \infty;1) \cup (4; + \infty).\]
\[\textbf{б)}\ |2x - 5| < x - 1\]
\[2x - 5 = 0\]
\[2x = 5\]
\[x = 2,5.\]
\[x \leq 2,5:\]
\[- 2x + 5 < x - 1\]
\[- 3x < - 6\]
\[x > 2.\]
\[x \in (2;2,5\rbrack.\]
\[x > 2,5:\]
\[2x - 5 < x - 1\]
\[x < 4.\]
\[x \in (2,5;4).\]
\[Объединим\ решения:\]
\[x \in (2;4).\]
\[Ответ:x \in (2;4).\]
\[\textbf{в)}\ |3x - 7| > 2x - 3\]
\[3x - 7 = 0\]
\[3x = 7\]
\[x = \frac{7}{3}\]
\[x = 2\frac{1}{3}.\]
\[x \leq 2\frac{1}{3}:\]
\[- 3x + 7 > 2x - 3\]
\[- 5x > - 10\]
\[x < 2.\]
\[x \in ( - \infty;2).\]
\[x > 2\frac{1}{3}:\]
\[3x - 7 > 2x - 3\]
\[x > 4.\]
\[x \in (4; + \infty).\]
\[Объединим\ решения:\]
\[x \in ( - \infty;2) \cup (4; + \infty).\]
\[Ответ:x \in ( - \infty;2) \cup (4; + \infty).\]
\[\textbf{г)}\ |2x - 7| < 0,5x + 2\]
\[2x - 7 = 0\]
\[2x = 7\]
\[x = 3,5.\]
\[x \leq 3,5:\]
\[- 2x + 7 < 0,5x + 2\]
\[- 2,5x < - 5\]
\[x > 2.\]
\[x \in (2;3,5\rbrack.\]
\[x > 3,5:\]
\[2x - 7 < 0,5x + 2\]
\[1,5x < 9\]
\[x < 6.\]
\[x \in (3,5\ ;6).\]
\[Объединим\ решения:\]
\[x \in (2;6).\]
\[Ответ:x \in (2;6).\]
\[\boxed{\mathbf{11.}}\]
\[\textbf{а)}\ \frac{|x - 1| + 10}{4|x - 1| + 3} > 2\]
\[x - 1 \geq 0\]
\[x \geq 1.\]
\[x - 1 < 0\]
\[x < 1.\]
\[x < 1:\]
\[\frac{1 - x + 10}{4(1 - x) + 3} > 2\]
\[\frac{11 - x}{4 - 4x + 3} > 2\]
\[\frac{11 - x}{7 - 4x} - 2 > 0\]
\[\frac{11 - x - 2(7 - 4x)}{7 - 4x} > 0\]
\[\frac{11 - x - 14 + 8x}{7 - 4x} > 0\]
\[\frac{7x - 3}{- 4x + 7} > 0\]
\[\frac{3}{7} < x < \frac{7}{4}.\]
\[x \in \left( \frac{3}{7};1 \right).\]
\[x \geq 1:\]
\[\frac{x - 1 + 10}{4(x - 1) + 3} > 2\]
\[\frac{x + 9}{4x - 4 + 3} > 2\]
\[\frac{x + 9}{4x - 1} - 2 > 0\]
\[\frac{x + 9 - 2(4x - 1)}{4x - 1} > 0\]
\[\frac{x + 9 - 8x + 2}{4x - 1} > 0\]
\[\frac{11 - 7x}{4x - 1} > 0\]
\[\frac{1}{4} < x < \frac{11}{7}.\]
\[x \in \left\lbrack 1;\frac{11}{7} \right).\]
\[Объединим\ решения:\ \]
\[x \in \left( \frac{3}{7};\frac{7}{11} \right).\]
\[Ответ:\ x \in \left( \frac{3}{7};\frac{7}{11} \right).\]
\[\textbf{б)}\ \frac{|x - 2| + 8}{3|x - 2| + 1} < 3\]
\[x - 2 \geq 0\]
\[x \geq 2.\]
\[x - 2 < 0\]
\[x < 2.\]
\[x < 2:\]
\[\frac{2 - x + 8}{3(2 - x) + 1} < 3\]
\[\frac{10 - x}{6 - 3x + 1} - 3 < 0\]
\[\frac{10 - x}{7 - 3x} - 3^{\backslash 7 - 3x} < 0\]
\[\frac{10 - x - 21 + 9x}{7 - 3x} < 0\]
\[\frac{8x - 11}{7 - 3x} < 0\]
\[x < \frac{11}{8};\ \ \ x > \frac{7}{3}.\]
\[x \in \left( - \infty;\frac{11}{8} \right).\]
\[x \geq 2:\]
\[\frac{x - 2 + 8}{3(x - 2) + 1} < 3\]
\[\frac{x + 6}{3x - 6 + 1} < 3\]
\[\frac{x + 6}{3x - 5} - 3^{\backslash 3x - 5} < 0\]
\[\frac{x + 6 - 9x + 15}{3x - 5} < 0\]
\[\frac{21 - 8x}{3x - 5} < 0\]
\[x < \frac{5}{3};\ \ \ x > \frac{21}{8}.\]
\[x \in \left( \frac{21}{8}; + \infty \right).\]
\[Объединим\ решения:\ \]
\[x \in \left( - \infty;\frac{11}{8} \right) \cup \left( \frac{21}{8}; + \infty \right).\]
\[Ответ:\ x \in \left( - \infty;\frac{11}{8} \right) \cup \left( \frac{21}{8}; + \infty \right).\]
\[\textbf{в)}\ \frac{|x - 3| + 6}{2|x - 3| + 1} < 4\]
\[x - 3 \geq 0\]
\[x \geq 3.\]
\[x - 3 < 0\]
\[x < 3.\]
\[x < 3:\]
\[\frac{3 - x + 6}{2(3 - x) + 1} < 4\]
\[\frac{9 - x}{6 - 2x + 1} < 4\]
\[\frac{9 - x}{7 - 2x} - 4^{\backslash 7 - 2x} < 0\]
\[\frac{9 - 2x - 28 + 8x}{7 - 2x} < 0\]
\[\frac{7x - 19}{7 - 2x} < 0\]
\[x < \frac{19}{7};\ \ x > \frac{7}{2}.\]
\[x \in \left( - \infty;\frac{19}{7} \right).\]
\[x \geq 3:\]
\[\frac{x - 3 + 6}{2(x - 3) + 1} < 4\]
\[\frac{x + 3}{2x - 6 + 1} < 4\]
\[\frac{x + 3}{2x - 5} - 4^{\backslash 2x - 5} < 0\]
\[\frac{x + 3 - 8x + 20}{2x - 5} < 0\]
\[\frac{23 - 7x}{2x - 5} < 0\]
\[x < \frac{5}{2};\ \ x > \frac{23}{7}.\]
\[x \in \left( \frac{23}{7}; + \infty \right).\]
\[Объединим\ решения:\ \]
\[x \in \left( - \infty;\frac{19}{7} \right) \cup \left( \frac{23}{7}; + \infty \right).\]
\[Ответ:\ x \in \left( - \infty;\frac{19}{7} \right) \cup \left( \frac{23}{7}; + \infty \right).\]
\[\textbf{г)}\ \frac{|x - 2| + 7}{3|x - 2| + 2} > 1\]
\[x - 2 \geq 0\]
\[x \geq 2.\]
\[x - 2 < 0\]
\[x < 2.\]
\[x < 2:\]
\[\frac{2 - x + 7}{3(2 - x) + 2} > 1\]
\[\frac{9 - x}{6 - 3x + 2} > 1\]
\[\frac{9 - x}{8 - 3x} - 1^{\backslash 8 - 3x} > 0\]
\[\frac{9 - x - 8 + 3x}{8 - 3x} > 0\]
\[\frac{2x + 1}{8 - 3x} > 0\]
\[- \frac{1}{2} < x < \frac{8}{3}.\]
\[x \in \left( - \frac{1}{2};2 \right).\]
\[x \geq 2:\]
\[\frac{x - 2 + 7}{3(x - 2) + 2} > 1\]
\[\frac{x + 5}{3x - 6 + 2} > 1\]
\[\frac{x + 5}{3x - 4} - 1^{\backslash 3x - 4} > 0\]
\[\frac{x + 5 - 3x + 4}{3x - 4} > 0\]
\[\frac{9 - 2x}{3x - 4} > 0\]
\[\frac{4}{3} < x < \frac{9}{2}.\]
\[x \in \left\lbrack 2;\frac{9}{2} \right).\]
\[Объединим\ решения:\ \]
\[x \in \left( - \frac{1}{2};\frac{9}{2} \right).\]
\[Ответ:\ x \in ( - 0,5;4,5).\]
\[\boxed{\mathbf{12.}}\]
\[\textbf{а)}\ |x + 1| + |x + 3| < 8\]
\[x = - 1;\ \ x = - 3.\]
\[x < - 3:\]
\[- x - 1 - x - 3 < 8\]
\[- 2x < 12\]
\[x > - 6.\]
\[x \in ( - 6;\ - 3).\]
\[- 3 \leq x \leq - 1:\]
\[- x - 1 + x + 3 < 8\]
\[0x < 6.\]
\[x \in \lbrack - 3; - 1\rbrack.\]
\[x > - 1:\]
\[x + 1 + x + 3 < 8\]
\[2x < 4\]
\[x < 2.\]
\[x \in ( - 1;2).\]
\[Объединим\ решения:\ \]
\[x \in ( - 6;2).\]
\[Ответ:\ x \in ( - 6;2).\]
\[\textbf{б)}\ |x + 2| + |x + 4| < 6\]
\[x = - 2;\ \ x = - 4.\]
\[x < - 4:\]
\[- x - 2 - x - 4 < 6\]
\[- 2x < 12\]
\[x > - 6.\]
\[x \in ( - 6; - 4).\]
\[- 4 \leq x \leq - 2:\]
\[- x - 2 + x + 4 < 6\]
\[0x < 8.\]
\[x \in \lbrack - 4; - 2\rbrack.\]
\[x > - 2:\]
\[x + 2 + x + 4 < 6\]
\[2x < 0\]
\[x < 0.\]
\[x \in ( - 2;0).\]
\[Объединим\ решения:\ \]
\[x \in ( - 6;0).\]
\[Ответ:\ x \in ( - 6;0).\]
\[\textbf{в)}\ |x + 3| + |x - 2| > 5\]
\[x = - 3;\ \ x = 2.\]
\[x < - 3:\]
\[- x - 3 + 2 - x > 5\]
\[- 2x > 6\]
\[x < - 3.\]
\[x \in ( - \infty; - 3).\]
\[- 3 \leq x \leq 2:\]
\[x + 3 + 2 - x > 5\]
\[0x > 0\]
\[нет\ решений.\]
\[x > 2:\]
\[x + 3 + x - 2 > 5\]
\[2x > 4\]
\[x > 2.\]
\[x \in (2; + \infty).\]
\[Объединим\ решения:\ \]
\[x \in ( - \infty; - 3) \cup (2; + \infty).\]
\[Ответ:\ x \in ( - \infty; - 3) \cup (2; + \infty).\]
\[\textbf{г)}\ |x + 7| + |x + 1| > 9\]
\[x = - 7;\ \ \ x = - 1.\]
\[x < - 7:\]
\[- x - 7 - x - 1 > 9\]
\[- 2x > 17\]
\[x < - 8,5.\]
\[x \in ( - \infty; - 8,5).\]
\[- 7 \leq x \leq - 1:\]
\[x + 7 - x - 1 > 9\]
\[0x > 3\]
\[нет\ корней.\]
\[x > - 1:\]
\[x + 7 + x + 1 > 9\]
\[2x > 1\]
\[x > 0,5.\]
\[x \in (0,5; + \infty).\]
\[Объединим\ решения:\ \]
\[x \in ( - \infty; - 8,5) \cup (0,5; + \infty).\]
\[Ответ:\ x \in ( - \infty; - 8,5) \cup (0,5; + \infty).\]
\[\boxed{\mathbf{13.}}\]
\[\textbf{а)}\ \left| x^{2} - 9 \right| + |x + 4| \geq 7\]
\[x^{2} - 9 = 0\]
\[x = \pm 3.\]
\[x + 4 = 0\]
\[x = - 4.\]
\[x \leq - 4:\]
\[x^{2} - 9 - x - 4 \geq 7\]
\[x^{2} - x - 13 - 7 \geq 0\]
\[x^{2} - x - 20 \geq 0\]
\[x_{1} + x_{2} = 1;\ \ x_{1} \cdot x_{2} = - 20\]
\[x_{1} = 5;\ \ \ x_{2} = - 4;\]
\[(x + 4)(x - 5) \geq 0\]
\[x \leq - 4;\ \ \ x \geq 5.\]
\[x \in ( - \infty; - 4\rbrack.\]
\[- 4 < x < - 3:\]
\[x^{2} - 9 + x + 4 \geq 7\]
\[x^{2} + x - 5 - 7 \geq 0\]
\[x^{2} + x - 12 \geq 0\]
\[x_{1} + x_{2} = - 1;\ \ x_{1} \cdot x_{2} = - 12\]
\[x_{1} = - 4;\ \ x_{2} = 3;\]
\[(x + 4)(x - 3) \geq 0\]
\[x \leq - 4;\ \ x \geq 3.\]
\[Нет\ решений.\]
\[- 3 \leq x < 3:\]
\[- x^{2} + 9 + x + 4 \geq 7\]
\[- x^{2} + x + 13 - 7 \geq 0\]
\[- x^{2} + x + 6 \geq 0\]
\[x^{2} - x - 6 \leq 0\]
\[x_{1} + x_{2} = 1;\ \ x_{1} \cdot x_{2} = - 6\]
\[x_{1} = 3;\ \ \ x_{2} = - 2;\]
\[(x + 2)(x - 3) \leq 0\]
\[- 2 \leq x \leq 3.\]
\[x \in \lbrack - 2;3).\]
\[x \geq 3:\]
\[x^{2} - 9 + x + 4 \geq 7\]
\[x^{2} + x - 5 - 7 \geq 0\]
\[x^{2} + x - 12 \geq 0\]
\[x_{1} + x_{2} = - 1;\ \ x_{1} \cdot x_{2} = - 12\]
\[x_{1} = - 4;\ \ x_{2} = 3;\]
\[(x + 4)(x - 3) \geq 0\]
\[x \leq - 4;\ \ x \geq 3.\]
\[x \in \lbrack 3; + \infty).\]
\[Объединим\ решения:\ \]
\[x \in ( - \infty; - 4\rbrack \cup \lbrack - 2; + \infty).\]
\[Ответ:\ x \in ( - \infty; - 4\rbrack \cup \lbrack - 2; + \infty).\]
\[\textbf{б)}\ \left| x^{2} - 16 \right| + |x - 5| \geq 9\]
\[x^{2} - 16 = 0\]
\[x = \pm 4.\]
\[x - 5 = 0\]
\[x = 5.\]
\[x \leq - 4:\]
\[x^{2} - 16 + 5 - x \geq 9\]
\[x^{2} - x - 11 - 9 \geq 0\]
\[x^{2} - x - 20 \geq 0\]
\[x_{1} + x_{2} = 1;\ \ x_{1} \cdot x_{2} = - 20\]
\[x_{1} = 5;\ \ \ x_{2} = - 4;\]
\[(x + 4)(x - 5) \geq 0\]
\[x \leq - 4;\ \ \ x \geq 5.\]
\[x \in ( - \infty; - 4\rbrack.\]
\[- 4 < x < 4:\]
\[- x^{2} + 16 + 5 - x \geq 9\]
\[- x^{2} - x + 21 - 9 \geq 0\]
\[- x^{2} - x + 12 \geq 0\]
\[x^{2} + x - 12 \leq 0\]
\[x_{1} + x_{2} = - 1;\ \ x_{1} \cdot x_{2} = - 12\]
\[x_{1} = - 4;\ \ \ x_{2} = 3;\]
\[(x + 4)(x - 3) \leq 0\]
\[- 4 \leq x \leq 3.\]
\[x \in ( - 4;3\rbrack.\]
\[4 \leq x < 5:\]
\[x^{2} - 16 + 5 - x \geq 9\]
\[x^{2} - x - 11 - 9 \geq 0\]
\[x^{2} - x - 20 \geq 0\]
\[x_{1} + x_{2} = 1;\ \ x_{1} \cdot x_{2} = - 20\]
\[x_{1} = 5;\ \ \ x_{2} = - 4;\]
\[(x + 4)(x - 5) \geq 0\]
\[x \leq - 4;\ \ \ x \geq 5.\]
\[Нет\ решений.\]
\[x \geq 5:\]
\[x^{2} - 16 + x - 5 \geq 9\]
\[x^{2} + x - 21 - 9 \geq 0\]
\[x^{2} + x - 30 \geq 0\]
\[x_{1} + x_{2} = - 1;\ \ x_{1} \cdot x_{2} = - 30\]
\[x_{1} = - 6;\ \ x_{2} = 5.\]
\[x \leq - 6;\ \ x \geq 5.\]
\[x \in \lbrack 5; + \infty).\]
\[Объединим\ решения:\ \]
\[x \in ( - \infty;3\rbrack \cup \lbrack 5; + \infty).\]
\[Ответ:\ x \in ( - \infty;3\rbrack \cup \lbrack 5; + \infty).\]
\[\textbf{в)}\ \left| x^{2} - 4 \right| + |x - 3| \leq 5\]
\[x^{2} - 4 = 0\]
\[x = \pm 2.\]
\[x - 3 = 0\]
\[x = 3.\]
\[x \leq - 2:\]
\[x^{2} - 4 + 3 - x \leq 5\]
\[x^{2} - x - 1 - 5 \leq 0\]
\[x^{2} - x - 6 \leq 0\]
\[(x + 2)(x - 3) \leq 0\]
\[- 2 \leq x \leq 3.\]
\[x \in \left\{ - 2 \right\}.\]
\[- 2 < x < 2:\]
\[- x^{2} + 4 + 3 - x \leq 5\]
\[- x^{2} - x + 7 - 5 \leq 0\]
\[- x^{2} - x + 2 \leq 0\]
\[x^{2} + x - 2 \geq 0\]
\[(x + 2)(x - 1) \geq 0\]
\[x \leq - 2;\ \ x \geq 1.\]
\[x \in \lbrack 1;2).\]
\[2 \leq x < 3:\]
\[x^{2} - 4 + 3 - x \leq 5\]
\[x^{2} - x - 1 - 5 \leq 0\]
\[x^{2} - x - 6 \leq 0\]
\[(x + 2)(x - 3) \leq 0\]
\[- 2 \leq x \leq 3.\]
\[x \in \lbrack 2;3).\]
\[x \geq 3:\]
\[x^{2} - 4 + x - 3 \leq 5\]
\[x^{2} + x - 7 - 5 \leq 0\]
\[x^{2} + x - 12 \leq 0\]
\[(x + 4)(x - 3) \leq 0\]
\[- 4 \leq x \leq 3.\]
\[x \in \left\{ 3 \right\}.\]
\[Объединим\ решения:\ \]
\[x \in \left\{ - 2 \right\} \cup \lbrack 1;3\rbrack.\]
\[Ответ:\ x \in \left\{ - 2 \right\} \cup \lbrack 1;3\rbrack.\]
\[\textbf{г)}\ \left| x^{2} - 1 \right| + |x - 2| \leq 3\]
\[x^{2} - 1 = 0\]
\[x = \pm 1.\]
\[x - 2 = 0\]
\[x = 2.\]
\[x \leq - 1:\]
\[x^{2} - 1 + 2 - x - 3 \leq 0\]
\[x^{2} - x - 2 \leq 0\]
\[(x + 1)(x - 2) \leq 0\]
\[- 1 \leq x \leq 2.\]
\[x \in \left\{ - 1 \right\}.\]
\[- 1 < x < 1:\]
\[- x^{2} + 1 + 2 - x - 3 \leq 0\]
\[- x^{2} - x \leq 0\]
\[- x(x + 1) \leq 0\]
\[x(x + 1) \geq 0\]
\[x \leq - 1;\ \ \ x \geq 0.\]
\[x \in \lbrack 0;1).\]
\[1 \leq x < 2:\]
\[x^{2} - 1 + 2 - x - 3 \leq 0\]
\[x^{2} - x - 2 \leq 0\]
\[(x + 1)(x - 2) \leq 0\]
\[- 1 \leq x \leq 2.\]
\[x \in \lbrack 1;2).\]
\[x \geq 2:\]
\[x^{2} - 1 + x - 2 \leq 3\]
\[x^{2} + x - 1 - 2 - 3 \leq 0\]
\[x^{2} + x - 6 \leq 0\]
\[(x + 3)(x - 2) \leq 0\]
\[- 3 \leq x \leq 2.\]
\[x \in \left\{ 2 \right\}.\]
\[Объединим\ решения:\ \]
\[x \in \left\{ - 1 \right\} \cup \lbrack 0;2\rbrack.\]
\[Ответ:\ x \in \left\{ - 1 \right\} \cup \lbrack 0;2\rbrack.\]
\[\boxed{\mathbf{14.}}\]
\[\textbf{а)}\ \frac{|x - 1|}{x - 1} + \frac{|x - 2|}{x - 2} \geq 0\]
\[x = 1;\ \ \ x = 2.\]
\[x < 1:\]
\[- \frac{x - 1}{x - 1} - \frac{x - 2}{x - 2} \geq 0\]
\[- 1 - 1 \geq 0\]
\[- 2 \geq 0\]
\[нет\ корней.\]
\[1 < x < 2:\]
\[\frac{x - 1}{x - 1} - \frac{x - 2}{x - 2} \geq 0\]
\[1 - 1 \geq 0\]
\[0 \geq 0\]
\[x \in (1;2).\]
\[x > 2:\]
\[\frac{x - 1}{x - 1} + \frac{x - 2}{x - 2} \geq 0\]
\[1 + 1 \geq 0\]
\[2 \geq 0\]
\[x \in (2; + \infty).\]
\[Объединим\ решения:\ \]
\[x \in (1;2) \cup (2; + \infty).\]
\[Ответ:\ x \in (1;2) \cup (2; + \infty).\]
\[\textbf{б)}\ \frac{|x - 5|}{x - 5} + \frac{|x - 6|}{x - 6} \geq 2\]
\[x = 5;\ \ x = 6.\]
\[x < 5:\]
\[- \frac{x - 5}{x - 5} - \frac{x - 6}{x - 6} \geq 2\]
\[- 1 - 1 \geq 2\]
\[- 2 \geq 2\]
\[Нет\ корней.\]
\[5 < x < 6:\]
\[\frac{x - 5}{x - 5} - \frac{x - 6}{x - 6} \geq 2\]
\[1 - 1 \geq 2\]
\[0 \geq 2\]
\[нет\ корней.\]
\[x > 6:\]
\[\frac{x - 5}{x - 5} + \frac{x - 6}{x - 6} \geq 2\]
\[1 + 1 \geq 2\]
\[2 \geq 2\]
\[x \in (6; + \infty).\]
\[Объединим\ решения:\ \]
\[x \in (6; + \infty).\]
\[Ответ:\ x \in (6; + \infty).\]
\[\textbf{в)}\ \frac{|x - 5| - |x - 3|}{|x - 2| + x - 2} \geq 0\]
\[|x - 2| + x - 2 \neq 0\]
\[|x - 2| \neq - (x - 2)\]
\[x > 2.\]
\[x = 5;\ \ \ x = 3.\]
\[2 < x < 3:\]
\[\frac{5 - x - 3 + x}{x - 2 + x - 2} \geq 0\]
\[\frac{2}{2x - 4} \geq 0\]
\[\frac{1}{x - 2} \geq 0\]
\[x > 2.\]
\[x \in (2;3).\]
\[3 \leq x < 5:\]
\[\frac{5 - x - x + 3}{x - 2 + x - 2} \geq 0\]
\[\frac{- 2x + 8}{2x - 4} \geq 0\]
\[\frac{- x + 4}{x - 2} \geq 0\]
\[4 - x \geq 0\]
\[x \leq 4.\]
\[x \in \lbrack 3;4\rbrack.\]
\[x \geq 5:\]
\[\frac{x - 5 - x + 3}{x - 2 + x - 2} \geq 0\]
\[\frac{- 2}{2x - 4} \geq 0\]
\[- \frac{1}{x - 2} \geq 0\]
\[решений\ нет.\]
\[Объединим\ решения:\ \]
\[x \in (2;4\rbrack.\]
\[Ответ:\ x \in (2;4\rbrack.\]
\[\textbf{г)}\ \frac{|x - 7| - |x - 3|}{x - 8 - |x - 8|} \geq 0\]
\[x - 8 - |x - 8| \neq 0\]
\[|x - 8| \neq x - 8\]
\[x < 8.\]
\[x = 7;\ \ \ x = 3.\]
\[x < 3:\]
\[\frac{7 - x - 3 + x}{x - 8 - 8 + x} \geq 0\]
\[\frac{4}{2x - 16} \geq 0\]
\[\frac{2}{x - 8} \geq 0\]
\[x < 8 - решений\ нет.\]
\[3 \leq x < 7:\]
\[\frac{7 - x - x + 3}{x - 8 - 8 + x} \geq 0\]
\[\frac{10 - 2x}{12x - 16} \geq 0\]
\[\frac{5 - x}{x - 8} \geq 0\]
\[5 - x \leq 0\]
\[x \geq 5.\]
\[x \in \lbrack 5;7).\]
\[7 \leq x < 8:\]
\[\frac{x - 7 - x + 3}{x - 8 - 8 + x} \geq 0\]
\[\frac{- 4}{2x - 16} \geq 0\]
\[\frac{4}{2x - 16} \leq 0\]
\[\frac{2}{x - 8} \leq 0\]
\[x \in \lbrack 7;8).\]
\[Объединим\ решения:\ \]
\[x \in \lbrack 5;8).\]
\[Ответ:\ x \in \lbrack 5;8).\]
\[\boxed{\mathbf{15.}}\]
\[\textbf{а)}\ 2|x|\left( x^{2} - 4x + 3 \right) + x\left| x^{2} - 4x + 3 \right| > 0\]
\[x^{2} - 4x + 3 = 0\]
\[D_{1} = 4 - 3 = 1\]
\[x_{1} = 2 + 1 = 3;\]
\[x_{2} = 2 - 1 = 1.\]
\[x < 0:\]
\[- 2x\left( x^{2} - 4x + 3 \right) + x\left( x^{2} - 4x + 3 \right) > 0\]
\[\left( x^{2} - 4x + 3 \right)(x - 2x) > 0\]
\[- x\left( x^{2} - 4x + 3 \right) > 0\]
\[- x > 0\]
\[x < 0.\]
\[x \in ( - \infty;0).\]
\[0 \leq x < 1:\]
\[2x\left( x^{2} - 4x + 3 \right) + x\left( x^{2} - 4x + 3 \right) > 0\]
\[\left( x^{2} - 4x + 3 \right)(2x + x) > 0\]
\[3x\left( x^{2} - 4x + 3 \right) > 0\]
\[x > 0.\]
\[x \in (0;1).\]
\[1 \leq x < 3:\]
\[2x\left( x^{2} - 4x + 3 \right) - x\left( x^{2} - 4x + 3 \right) > 0\]
\[\left( x^{2} - 4x + 3 \right)(2x - x) > 0\]
\[x\left( x^{2} - 4x + 3 \right) > 0\]
\[x^{2} - 4x + 3 \leq 0;\ \ x < 0;\]
\[Нет\ решений.\]
\[x \geq 3:\]
\[2x\left( x^{2} - 4x + 3 \right) + x\left( x^{2} - 4x + 3 \right) > 0\]
\[\left( x^{2} - 4x + 3 \right)(2x + x) > 0\]
\[3x\left( x^{2} - 4x + 3 \right) > 0\]
\[x > 0.\]
\[x \in (3; + \infty).\]
\[Объединим\ решения:\ \]
\[x \in ( - \infty;0) \cup (0;1) \cup (3; + \infty).\]
\[Ответ:\ x \in ( - \infty;0) \cup (0;1) \cup (3; + \infty).\]
\[\textbf{б)}\ 2|x - 1|\left( x^{2} - 4x + 3 \right) + (x - 1)\left| x^{2} - 4x + 3 \right| < 0\]
\[x - 1 = 0\]
\[x = 1.\]
\[x^{2} - 4x + 3 = 0\]
\[D_{1} = 4 - 3 = 1\]
\[x_{1} = 2 + 1 = 3;\]
\[x_{2} = 2 - 1 = 1.\]
\[x \leq 1:\]
\[- 2(x - 1)\left( x^{2} - 4x + 3 \right) + (x - 1)\left( x^{2} - 4x + 3 \right) < 0\]
\[- (x - 1)\left( x^{2} - 4x + 3 \right) < 0\]
\[(x - 1)\left( x^{2} - 4x + 3 \right) > 0\]
\[x - 1 > 0\]
\[x > 1.\]
\[Нет\ решений.\]
\[1 < x < 3:\]
\[2(x - 1)\left( x^{2} - 4x + 3 \right) - (x - 1)\left( x^{2} - 4x + 3 \right) < 0\]
\[(x - 1)\left( x^{2} - 4x + 3 \right) < 0\]
\[x - 1 > 0\]
\[x > 1.\]
\[x \in (1;3).\]
\[x \geq 3:\]
\[2(x - 1)\left( x^{2} - 4x + 3 \right) + (x - 1)\left( x^{2} - 4x + 3 \right) < 0\]
\[3(x - 1)\left( x^{2} - 4x + 3 \right) < 0\]
\[x - 1 < 0\]
\[x < 1.\]
\[Нет\ решений.\]
\[Объединим\ решения:\ \]
\[x \in (1;3).\]
\[Ответ:\ x \in (1;3).\]
\[\textbf{в)}\ 2|x|\left( x^{2} - 5x + 6 \right) + x\left| x^{2} - 5x + 6 \right| \leq 0\]
\[x^{2} - 5x + 6 = 0\]
\[x_{1} + x_{2} = 5;\ \ x_{1} \cdot x_{2} = 6\]
\[x_{1} = 2;\ \ \ x_{2} = 3.\]
\[x < 0:\]
\[- 2x\left( x^{2} - 5x + 6 \right) + x\left( x^{2} - 5x + 6 \right) \leq 0\]
\[- x\left( x^{2} - 5x + 6 \right) \leq 0\]
\[- x \leq 0\]
\[x \geq 0.\]
\[Решений\ нет.\]
\[0 \leq x < 2:\]
\[2x\left( x^{2} - 5x + 6 \right) + x\left( x^{2} - 5x + 6 \right) \leq 0\]
\[3x\left( x^{2} - 5x + 6 \right) \leq 0\]
\[3x \leq 0\]
\[x \leq 0.\]
\[x \in \left\{ 0 \right\}.\]
\[2 \leq x \leq 3:\]
\[2x\left( x^{2} - 5x + 6 \right) - x\left( x^{2} - 5x + 6 \right) \leq 0\]
\[x\left( x^{2} - 5x + 6 \right) \leq 0\]
\[x \geq 0.\]
\[x \in \lbrack 2;3\rbrack.\]
\[x > 3:\]
\[2x\left( x^{2} - 5x + 6 \right) + x\left( x^{2} - 5x + 6 \right) \leq 0\]
\[3x\left( x^{2} - 5x + 6 \right) \leq 0\]
\[3x \leq 0\]
\[x \leq 0.\]
\[Решений\ нет.\]
\[Объединим\ решения:\ \]
\[x \in \left\{ 0 \right\} \cup \lbrack 2;3\rbrack.\]
\[Ответ:\ x \in \left\{ 0 \right\} \cup \lbrack 2;3\rbrack.\]
\[\textbf{г)}\ 2|x - 1|\left( x^{2} - 5x + 6 \right) + (x - 1)\left| x^{2} - 5x + 6 \right| \leq 0\]
\[x - 1 = 0\]
\[x = 1.\]
\[x^{2} - 5x + 6 = 0\]
\[x_{1} + x_{2} = 5;\ \ x_{1} \cdot x_{2} = 6\]
\[x_{1} = 2;\ \ \ x_{2} = 3.\]
\[x \leq 1:\]
\[- 2(x - 1)\left( x^{2} - 5x + 6 \right) + (x - 1)\left( x^{2} - 5x + 6 \right) \leq 0\]
\[- (x - 1)\left( x^{2} - 5x + 6 \right) \leq 0\]
\[(x - 1)\left( x^{2} - 5x + 6 \right) \geq 0\]
\[x - 1 \geq 0\]
\[x \geq 1.\]
\[x \in \left\{ 1 \right\}.\]
\[1 < x < 2:\]
\[2(x - 1)\left( x^{2} - 5x + 6 \right) + (x - 1)\left( x^{2} - 5x + 6 \right) \leq 0\]
\[3(x - 1)\left( x^{2} - 5x + 6 \right) \leq 0\]
\[x - 1 \leq 0\]
\[x \leq 1.\]
\[Нет\ решений.\]
\[2 \leq x \leq 3:\]
\[2(x - 1)\left( x^{2} - 5x + 6 \right) - (x - 1)\left( x^{2} - 5x + 6 \right) \leq 0\]
\[(x - 1)\left( x^{2} - 5x + 6 \right) \leq 0\]
\[x - 1 > 0\]
\[x > 1.\]
\[x \in \lbrack 2;3\rbrack.\]
\[x > 3:\]
\[2(x - 1)\left( x^{2} - 5x + 6 \right) + (x - 1)\left( x^{2} - 5x + 6 \right) \leq 0\]
\[3(x - 1)\left( x^{2} - 5x + 6 \right) \leq 0\]
\[x - 1 \leq 0\]
\[x \leq 1.\]
\[Нет\ решений.\]
\[Объединим\ решения:\ \]
\[x \in \left\{ 1 \right\} \cup \lbrack 2;3\rbrack.\]
\[Ответ:\ x \in \left\{ 1 \right\} \cup \lbrack 2;3\rbrack.\]
\[\boxed{\mathbf{16.}}\]
\[\textbf{а)}\ (x + 2) \cdot 2^{2 - |x - 2|} - x < (x + 1) \cdot \left| 2^{x} - 1 \right| + 2^{x} + 1\]
\[x - 2 = 0\]
\[x = 2.\]
\[2^{x} - 1 = 0\]
\[2^{x} = 1\]
\[x = 0.\]
\[x < 0:\]
\[(x + 2) \cdot 2^{2 - 2 + x} - x < (x + 1) \cdot \left( 1 - 2^{x} \right) + 2^{x} + 1\]
\[(x + 2) \cdot 2^{x} - x < x + 1 - x \cdot 2^{x} - 2^{x} + 2^{x} + 1\]
\[x \cdot 2^{x} + 2 \cdot 2^{x} - x < x + 2 - x \cdot 2^{x}\]
\[2x \cdot 2^{x} + 2 \cdot 2^{x} - 2x - 2 < 0\]
\[2x\left( 2^{x} - 1 \right) + 2\left( 2^{x} - 1 \right) < 0\]
\[\left( 2^{x} - 1 \right)(2x + 2) < 0\]
\[2(x + 1)\left( 2^{x} - 1 \right) < 0\]
\[2^{x} - 1 < 0;\]
\[x + 1 > 0\]
\[x > - 1.\]
\[x \in ( - 1;0).\]
\[0 \leq x \leq 2:\]
\[(x + 2) \cdot 2^{2 - 2 + x} - x < (x + 1) \cdot \left( 2^{x} - 1 \right) + 2^{x} + 1\]
\[(x + 2) \cdot 2^{x} - x < x \cdot 2^{x} + 2^{x} - x - 1 + 2^{x} + 1\]
\[x \cdot 2^{x} + 2 \cdot 2^{x} - x < x \cdot 2^{x} + 2 \cdot 2^{x} - x\]
\[0 < 0\]
\[Нет\ решений.\]
\[x > 2:\]
\[(x + 2) \cdot 2^{2 - x + 2} - x < (x + 1) \cdot \left( 2^{x} - 1 \right) + 2^{x} + 1\]
\[(x + 2) \cdot 2^{4 - x} - x < x \cdot 2^{x} + 2^{x} - x - 1 + 2^{x} + 1\]
\[(x + 2) \cdot 2^{4 - x} < (x + 2) \cdot 2^{x}\]
\[2^{4 - x} < 2^{x}\]
\[4 - x < x\]
\[2x > 4\]
\[x > 2.\]
\[x \in (2; + \infty).\]
\[Объединим\ решения:\]
\[x \in ( - 1;0) \cup (2; + \infty).\]
\[Ответ:x \in ( - 1;0) \cup (2; + \infty).\]
\[\textbf{б)}\ (x + 2) \cdot 4^{1 - |x - 1|} - x < (x + 1) \cdot \left| 4^{x} - 1 \right| + 4^{x} + 1\]
\[x - 1 = 0\]
\[x = 1.\]
\[4^{x} - 1 = 0\]
\[4^{x} = 1\]
\[x = 0.\]
\[x < 0:\]
\[(x + 2) \cdot 4^{1 - 1 + x} - x < (x + 1)\left( 1 - 4^{x} \right) + 4^{x} + 1\]
\[(x + 2) \cdot 4^{x} - x < x + 1 - x \cdot 4^{x} - 4^{x} + 4^{x} + 1\]
\[x \cdot 4^{x} + 2 \cdot 4^{x} - x < x + 2 - x \cdot 4^{x}\]
\[x \cdot 4^{x} + 2 \cdot 4^{x} - x - x - 2 + x \cdot 4^{x} < 0\]
\[2x \cdot 4^{x} + 2 \cdot 4^{x} - 2x - 2 < 0\]
\[2x\left( 4^{x} - 1 \right) + 2\left( 4^{x} - 1 \right) < 0\]
\[2(x + 1)\left( 4^{x} - 1 \right) < 0\]
\[4^{x} - 1 < 0;\ \]
\[x + 1 > 0\]
\[x > - 1.\]
\[x \in ( - 1;0).\]
\[0 \leq x \leq 1:\]
\[(x + 2) \cdot 4^{1 - 1 + x} - x < (x + 1)\left( 4^{x} - 1 \right) + 4^{x} + 1\]
\[(x + 2) \cdot 4^{x} - x < x \cdot 4^{x} + 4^{x} - x - 1 + 4^{x} + 1\]
\[x \cdot 4^{x} + 2 \cdot 4^{x} - x < x \cdot 4^{x} + 2 \cdot 4^{x} - x\]
\[x \cdot 4^{x} + 2 \cdot 4^{x} - x - x \cdot 4^{x} - 2 \cdot 4^{x} + x < 0\]
\[0 < 0.\]
\[Нет\ решений.\]
\[x > 1:\]
\[(x + 2) \cdot 4^{1 - x + 1} - x < (x + 1)\left( 4^{x} - 1 \right) + 4^{x} + 1\]
\[(x + 2) \cdot 4^{2 - x} - x < x \cdot 4^{x} + 4^{x} - x - 1 + 4^{x} + 1\]
\[x \cdot 4^{x} + 2 \cdot 4^{x} - x < x \cdot 4^{x} + 2 \cdot 4^{x} - x\]
\[(x + 2) \cdot 4^{2 - x} < (x + 2) \cdot 4^{x}\]
\[4^{2 - x} < 4^{x}\]
\[2 - x < x\]
\[2x > 2\]
\[x > 1.\]
\[x \in (1; + \infty).\]
\[Объединим\ решения:\]
\[x \in ( - 1;0) \cup (1; + \infty).\]
\[Ответ:x \in ( - 1;0) \cup (1; + \infty).\]
\[\boxed{\mathbf{17.}}\]
\[\frac{(x - 3)(x + 1)}{x\sqrt{x + 5}} > 0\]
\[1)\ Область\ определения:\]
\[x + 5 > 0\]
\[x > - 5.\]
\[x \neq 0.\]
\[M = ( - 5;0) \cup (0; + \infty).\]
\[2)\ Нули\ функции:\]
\[x = 3;\ \ x = - 1.\]
\[M_{1} = ( - 5; - 1) \cup ( - 1;0) \cup (0;3) \cup (3; + \infty).\]
\[3)\ Функция\ непрерывна\ на\ каждом\ из\ этих\ интервалов.\]
\[Отметим\ на\ координатной\ оси\ полученные\ точки:\]

\[4)\ Решим\ неравенство\ на\ каждом\ промежутке:\]
\[- 4 \in ( - 5; - 1);\ \ f( - 4) < 0;\]
\[- 0,5 \in ( - 1;0);\ \ f( - 0,5) > 0;\]
\[1 \in (0;3);\ \ \ \ \ \ \ \ \ \ \ f(1) < 0;\]
\[5 \in (3; + \infty);\ \ \ \ \ f(5) > 0.\]
\[5)\ Решение\ неравенства - это\ объединение\ интервалов:\]
\[( - 1;0) \cup (3; + \infty).\]
\[\boxed{\mathbf{18.}}\]
\[\textbf{а)}\ \frac{(x - 2)\left( x^{2} - 2x + 11 \right)}{x - 7} > 0\]
\[1)\ x - 7 \neq 0\]
\[x \neq 7.\]
\[2)\ x - 2 = 0\]
\[x = 2.\]
\[x^{2} - 2x + 11 = 0\]
\[D_{1} = 1 - 11 = - 10 < 0\]
\[корней\ нет.\]
\[M = ( - \infty;2) \cup (2;7) \cup (7; + \infty).\]
\[3)\ f(0) = \frac{- 2 \cdot 11}{- 7} = \frac{22}{7} > 0.\]
\[f(3) = \frac{1 \cdot (9 - 6 + 11)}{3 - 7} = \frac{14}{- 4} < 0.\]
\[f(\ 8) = \frac{6 \cdot (64 - 16 + 11)}{1} = 6 \cdot 59 > 0.\]

\[x \in ( - \infty;2) \cup (7; + \infty).\]
\[Ответ:x \in ( - \infty;2) \cup (7; + \infty)\text{.\ }\]
\[\textbf{б)}\ \frac{(x - 3)(x^{2} - 5x + 8)}{x + 1} < 0\]
\[1)\ x + 1 \neq 0\]
\[x \neq - 1.\]
\[2)\ x - 3 = 0\]
\[x = 3.\]
\[x^{2} - 5x + 8 = 0\]
\[D = 25 - 40 = - 15 < 0.\]
\[нет\ корней.\]
\[M = ( - \infty; - 1) \cup ( - 1;3) \cup (3; + \infty).\]
\[3)\ f( - 2) = \frac{- 5(4 + 10 + 8)}{- 2 + 1} = 5 \cdot 22 > 0.\]
\[f(0) = \frac{- 3 \cdot 8}{1} = - 24 < 0.\]
\[f(4) = \frac{(4 - 3)(16 - 20 + 8)}{4 + 1} = \frac{4}{5} > 0.\]

\[x \in ( - 1;3).\]
\[Ответ:x \in ( - 1;3).\]
\[\textbf{в)}\ \frac{(x - 3)\left( x^{2} - \pi x + 5 \right)}{x - 4} > 0\]
\[1)\ x - 4 \neq 0\]
\[x \neq 4.\]
\[2)\ x - 3 = 0\]
\[x = 3.\]
\[x^{2} - \pi x + 5 = 0\]
\[D = \pi^{2} - 20 < 0\]
\[корней\ нет.\]
\[M = ( - \infty;3) \cup (3;4) \cup (4; + \infty).\]
\[3)\ f(0) = \frac{- 3 \cdot 5}{- 4} = \frac{14}{4} > 0.\]
\[f(3,5) = \frac{(3,5 - 3)(12,25 - 15,5 + 5)}{3,5 - 4} = - 1,75 < 0.\]
\[f(5) = \frac{(5 - 3)(25 - 15,5 + 5)}{1} = 29 > 0.\]

\[x \in ( - \infty;3) \cup (4; + \infty).\]
\[Ответ:x \in ( - \infty;3) \cup (4; + \infty).\ \]
\[\textbf{г)}\ \frac{(x + 1)\left( x^{2} - ex + 4 \right)}{x + 5} < 0\]
\[1)\ x + 5 \neq 0\]
\[x \neq - 5.\]
\[2)\ x + 1 = 0\]
\[x = - 1.\]
\[x^{2} - ex + 4 = 0\]
\[D = e^{2} - 16 < 0\]
\[корней\ нет.\]
\[M = ( - \infty; - 5) \cup ( - 5; - 1) \cup ( - 1; + \infty).\]
\[3)\ f( - 6) = \frac{( - 6 + 1)(36 + 16,2 + 4)}{- 1} = 5 \cdot 56,2 > 0.\]
\[f( - 2) = \frac{( - 2 + 1)(4 + 5,4 + 4)}{- 2 + 5} = \frac{- (13,4)}{3} < 0.\]
\[f(0) = \frac{4}{5} > 0.\]

\[x \in ( - 5; - 1).\]
\[Ответ:x \in ( - 5; - 1).\]
\[\boxed{\mathbf{19.}}\]
\[\textbf{а)}\ \frac{\left( 2^{x} - 8 \right)\left( \lg x - 1 \right)}{\left( \log_{\frac{1}{2}}x + 1 \right)\sqrt{12 - x}} > 0\]
\[1)\ x > 0.\]
\[\log_{\frac{1}{2}}x + 1 \neq 0\]
\[\log_{\frac{1}{2}}x \neq - 1\]
\[x \neq 2.\]
\[12 - x > 0\]
\[x < 12.\]
\[2)\ 2^{x} - 8 = 0\]
\[2^{x} = 8\]
\[x = 3.\]
\[\lg x - 1 = 0\]
\[\lg x = 1\]
\[x = 10.\]
\[M = (0;2) \cup (2;3) \cup (3;10) \cup (10;12).\]
\[3)\ \]


\[= \frac{\left( \sqrt{32} - \sqrt{64} \right) \cdot \lg{0,25}}{\log_{0,5}{1,25}\sqrt{9,5}} < 0.\]



\[x \in (0;2) \cup (3;10).\]
\[Ответ:x \in (0;2) \cup (3;10).\]
\[\textbf{б)}\ \frac{\left( 3^{x} - 81 \right)\left( \log_{2}x - 2 \right)}{\left( \log_{\frac{1}{3}}x + 1 \right)\sqrt{5 - x}} < 0\]
\[1)\ x > 0.\]
\[\log_{\frac{1}{3}}x + 1 \neq 0\]
\[\log_{\frac{1}{3}}x \neq - 1\]
\[x \neq 3.\]
\[5 - x > 0\]
\[x < 5.\]
\[2)\ 3^{x} - 81 = 0\]
\[3^{x} = 81\]
\[3^{x} = 3^{4}\]
\[x = 4.\]
\[\log_{2}x - 2 = 0\]
\[\log_{2}x = 2\]
\[x = 4.\]
\[M = (0;3) \cup (3;4) \cup (4;5).\]
\[3)\ \]


\[= \frac{\left( \sqrt{2187} - \sqrt{6561} \right)\log_{2}{0,875}}{\log_{\frac{1}{3}}\frac{7}{6} \cdot \sqrt{1,5}} < 0.\]

\[= \frac{\left( \sqrt{3^{9}} - \sqrt{3^{8}} \right)\log_{2}{1,125}}{\log_{\frac{1}{3}}{1,5}\sqrt{0,5}} < 0.\]

\[x \in (3;4) \cup (4;5).\]
\[Ответ:x \in (3;4) \cup (4;5).\]
\[\textbf{в)}\ \frac{2^{\log_{2}(x - 1)} \cdot \left( \log_{0,2}x + 1 \right)}{|x - 4|\sqrt{6 - x}} > 0\]
\[1)\ x > 0.\]
\[x - 1 > 0\]
\[x > 1.\]
\[|x - 4| \neq 0\]
\[x \neq 4.\]
\[6 - x > 0\]
\[x < 6.\]
\[2)\ 2^{\log_{2}(x - 1)} = 0\]
\[нет\ корней.\]
\[\log_{0,2}x + 1 = 0\]
\[\log_{0,2}x = - 1\]
\[x = (0,2)^{- 1}\]
\[x = 5.\]
\[M = (1;4) \cup (4;5) \cup (5;6).\]
\[3)\ при\ x = R:\]
\[2^{\log_{2}(x - 1)} > 0;\ \ |x - 4| > 0;\ \ \sqrt{6 - x} > 0.\]
\[Нужно\ только\ на\ всех\ интервалах\ определить\ знак\ \]
\[множителя\ \ \left( \log_{0,2}x + 1 \right).\]
\[f(2) = \log_{0,2}2 + 1 = \log_{0,2}2 + \log_{0,2}{0,2} = \log_{0,2}{0,4} > 0.\]
\[f(4,5) = \log_{0,2}{4,5} + 1 = \log_{0,2}{4,5} + \log_{0,2}{0,2} = \log_{0,2}{0,9} > 0.\]
\[f(5,5) = \log_{0,2}{5,5} + 1 = \log_{0,2}{5,5} + \log_{0,2}{0,2} = \log_{0,2}{1,1} < 0.\]

\[x \in (1;4) \cup (4;5).\]
\[Ответ:x \in (1;4) \cup (4;5).\]
\[\textbf{г)}\ \frac{10^{\lg|x - 3|} \cdot \left( \log_{0,25}x + 1 \right)}{\left( \log_{2}x - 3 \right)\sqrt{8 - x}} < 0\]
\[1)\ x > 0.\]
\[|x - 3| \neq 0\]
\[x \neq 3.\]
\[\log_{2}x - 3 \neq 0\]
\[\log_{2}x \neq 3\]
\[x \neq 8.\]
\[8 - x > 0\]
\[x < 8.\]
\[2)\ 10^{\lg|x - 3|} = 0\]
\[нет\ корней.\]
\[\log_{0,25}x + 1 = 0\]
\[\log_{0,25}x = - 1\]
\[x = (0,25)^{- 1}\]
\[x = 4.\]
\[M = (0;3) \cup (3;4) \cup (4;8).\]
\[3)\ При\ x = R:\]
\[10^{\lg|x - 3|} > 0;\ \ \sqrt{8 - x} > 0.\]
\[Необходимо\ найти\ на\ интервалах\ знаки\ множителей\ \left( \log_{0,25}x + 1 \right)\ и\]
\[\left( \log_{2}x - 3 \right).\]




\[x \in (0;3) \cup (3;4).\]
\[Ответ:x \in (0;3) \cup (3;4).\]
\[\boxed{\mathbf{20.}}\]
\[\textbf{а)}\ \left( x^{2} - 4x \right)\sqrt{9 - x^{2}} \leq 0\]
\[1)\ 9 - x^{2} \geq 0\]
\[(x + 3)(x - 3) \leq 0\]
\[- 3 \leq x \leq 3.\]
\[2)\ x^{2} - 4x = 0\]
\[x(x - 4) = 0\]
\[x = 0;\ \ x = 4.\]
\[9 - x^{2} = 0\]
\[x^{2} = 9\]
\[x = \pm 3.\]
\[M = ( - 3;0) \cup (0;3).\]
\[3)\ f( - 1) = (1 + 4)\sqrt{9 - 1} = 5\sqrt{8} > 0.\]
\[f(1) = (1 - 4)\sqrt{9 - 1} = - 3\sqrt{8} < 0.\]

\[x \in \left\{ - 3 \right\} \cup \lbrack 0;3\rbrack\text{.\ }\]
\[\textbf{б)}\ \left( x^{2} - x - 30 \right)\sqrt{x^{2} - 4} \leq 0\]
\[1)\ x^{2} - 4 \geq 0\]
\[(x + 2)(x - 2) \geq 0\]
\[x \leq - 2;\ \ x \geq 2.\]
\[2)\ x^{2} - x - 30 = 0\]
\[x_{1} + x_{2} = 1;\ \ \ x_{1} \cdot x_{2} = - 30\]
\[x_{1} = - 5;\ \ \ \ x_{2} = 6.\]
\[x^{2} - 4 = 0\]
\[x^{2} = 4\]
\[x = \pm 2.\]
\[M = ( - \infty; - 5) \cup ( - 5; - 2) \cup (2;6) \cup (6; + \infty).\]
\[3)\ f( - 6) = (36 + 6 - 30)\sqrt{36 - 4} = 12\sqrt{32} > 0.\]
\[f( - 3) = (9 + 3 - 30)\sqrt{9 - 4} = - 18\sqrt{5} < 0.\]
\[f(4) = (16 - 4 - 30)\sqrt{16 - 4} = - 18\sqrt{12} < 0.\]
\[f(7) = (49 - 7 - 30)\sqrt{49 - 4} = 12\sqrt{45} > 0.\]

\[x \in \lbrack - 5; - 2\rbrack \cup \lbrack 2;6\rbrack.\]
\[Ответ:x \in \lbrack - 5; - 2\rbrack \cup \lbrack 2;6\rbrack.\]
\[\textbf{в)}\ \left( x^{2} - 6x + 8 \right)\sqrt{x^{2} - 9} \geq 0\]
\[1)\ x^{2} - 9 \geq 0\]
\[(x + 3)(x - 3) \geq 0\]
\[x \leq - 3;\ \ x \geq 3.\]
\[2)\ x^{2} - 6x + 8 = 0\]
\[D_{1} = 9 - 8 = 1\]
\[x_{1} = 3 + 1 = 4;\]
\[x_{2} = 3 - 1 = 2.\]
\[x^{2} - 9 = 0\]
\[x^{2} = 9\]
\[x = \pm 3.\]
\[M = ( - \infty; - 3) \cup (3;4) \cup (4; + \infty).\]
\[3)\ f( - 4) = (16 + 24 + 8)\sqrt{16 - 9} = 48\sqrt{7} > 0.\]
\[f(3,5) = (12,25 - 21 + 8)\sqrt{12,25 - 9} = - 0,75\sqrt{3,25} < 0.\]
\[f(5) = (25 - 30 + 8)\sqrt{25 - 9} = 3\sqrt{16} = 12 > 0.\]

\[x \in ( - \infty; - 3\rbrack \cup \left\{ 2 \right\} \cup \lbrack 4; + \infty).\]
\[Ответ:x \in ( - \infty; - 3\rbrack \cup \left\{ 2 \right\} \cup \lbrack 4; + \infty).\]
\[\textbf{г)}\ \left( x^{2} - x - 12 \right)\sqrt{x^{2} - 4} \geq 0\]
\[1)\ x^{2} - 4 \geq 0\]
\[(x + 2)(x - 2) \geq 0\]
\[x \leq - 2;\ \ x \geq 2.\]
\[2)\ x^{2} - x - 12 = 0\]
\[x_{1} + x_{2} = 1;\ \ \ x_{1} \cdot x_{2} = - 12\]
\[x_{1} = - 3;\ \ \ x_{2} = 4.\]
\[x^{2} - 4 = 0\]
\[x^{2} = 4\]
\[x = \pm 2.\]
\[M = ( - \infty; - 3) \cup ( - 3; - 2) \cup (2;4) \cup (4; + \infty).\]
\[3)\ f( - 6) = (36 + 6 - 12)\sqrt{36 - 4} = 30\sqrt{32} > 0.\]
\[f( - 2,5) = (6,25 + 2,5 - 12)\sqrt{6,25 - 4} = - 3,25\sqrt{2,25} < 0.\]
\[f(3) = (9 - 3 - 12)\sqrt{9 - 4} = - 6\sqrt{5} < 0.\]
\[f(6) = (36 - 6 - 12)\sqrt{36 - 4} = 18\sqrt{32} > 0.\]

\[x \in ( - \infty; - 3\rbrack \cup \left\{ - 2 \right\} \cup \{ 2\} \cup \lbrack 4; + \infty).\]
\[Ответ:x \in ( - \infty; - 3\rbrack \cup \left\{ - 2 \right\} \cup \{ 2\} \cup \lbrack 4; + \infty).\]
\[\boxed{\mathbf{21.}}\]
\[\textbf{а)}\ \frac{(x - 2)^{4}(1 + \log_{0,5}x)}{2x - 7} \leq 0\]
\[1)\ 2x - 7 \neq 0\]
\[2x \neq 7\]
\[x \neq 3,5.\]
\[x > 0.\]
\[2)\ (x - 2)^{4} = 0\]
\[x - 2 = 0\]
\[x = 2.\]
\[1 + \log_{0,5}x = 0\]
\[\log_{0,5}x = - 1\]
\[x = (0,5)^{- 1}\]
\[x = \left( \frac{1}{2} \right)^{- 1}\]
\[x = 2.\]
\[M = (0;2) \cup (2;3,5) \cup (3,5; + \infty).\]
\[3)\ f(1) = \frac{( - 1)^{4}\left( 1 + \log_{0,5}1 \right)}{2 - 7} = \frac{1 + 0}{- 5} = - \frac{1}{5} < 0.\]
\[f(3) = \frac{1^{4} \cdot \left( 1 + \log_{0,5}3 \right)}{6 - 7} = \frac{\log_{0,5}{0,5} + \log_{0,5}3}{- 1} = - \log_{0,5}{1,5} > 0.\]
\[f(4) = \frac{2^{4}\left( 1 + \log_{0,5}4 \right)}{8 - 7} = \frac{16 \cdot ( - 1)}{1} = - 16 < 0.\]

\[x \in (0;2\rbrack \cup (3,5; + \infty).\]
\[Ответ:x \in (0;2\rbrack \cup (3,5; + \infty).\]
\[\textbf{б)}\ \frac{(3x - 1)^{2}(x - 3)}{2^{x} - 4} \leq 0\]
\[1)\ 2^{x} - 4 \neq 0\]
\[2^{x} \neq 4\]
\[2^{x} \neq 2^{2}\]
\[x \neq 2.\]
\[2)\ (3x - 1)^{2} = 0\]
\[3x - 1 = 0\]
\[x = \frac{1}{3}.\]
\[x - 3 = 0\]
\[x = 3.\]
\[M = \left( - \infty;\frac{1}{3} \right) \cup \left( \frac{1}{3};2 \right) \cup (2;3) \cup (3; + \infty).\]
\[3)\ f(0) = \frac{( - 1)^{2} \cdot ( - 3)}{2^{0} - 4} = - \frac{3}{1 - 4} = 1 > 0.\]
\[f(1) = \frac{2^{2} \cdot ( - 2)}{2^{1} - 4} = \frac{- 8}{- 2} = 4 > 0.\]
\[f(2,5) = \frac{(7,5 - 1)^{2}( - 0,5)}{2^{2,5} - 4} = \frac{{6,5}^{2} \cdot ( - 0,5)}{\sqrt{32} - 4} = \frac{- 0,5 \cdot {6,5}^{2}}{4\sqrt{2} - 4} < 0.\]
\[f(4) = \frac{(12 - 1)^{2} \cdot 1}{2^{4} - 4} = \frac{11^{2}}{12} > 0.\]

\[x \in \left\{ \frac{1}{3} \right\} \cup (2;3\rbrack.\]
\[Ответ:x \in \left\{ \frac{1}{3} \right\} \cup (2;3\rbrack.\]
\[\textbf{в)}\ \frac{(x - 4)^{2}\left( 2 + \log_{\frac{1}{3}}x \right)}{x - 1} \leq 0\]
\[1)\ x - 1 \neq 0\]
\[x \neq 1.\]
\[x > 0.\]
\[2)\ (x - 4)^{2} = 0\]
\[x - 4 = 0\]
\[x = 4.\]
\[2 + \log_{\frac{1}{3}}x = 0\]
\[\log_{\frac{1}{3}}x = - 2\]
\[x = \left( \frac{1}{3} \right)^{- 2}\]
\[x = 9.\]
\[M = (0;1) \cup (1;4) \cup (4;9) \cup (9; + \infty).\]
\[3)\ f\left( \frac{1}{3} \right) = \frac{\left( - \frac{11}{3} \right)^{2}\left( 2 + \log_{\frac{1}{3}}\frac{1}{3} \right)}{\frac{1}{3} - 1\ } = \frac{\frac{121}{9} \cdot 3}{- \frac{2}{3}} = - \frac{121}{2} < 0.\]
\[f(3) = \frac{( - 1)^{2}\left( 2 + \log_{\frac{1}{3}}3 \right)}{3 - 1} = \frac{1 \cdot (2 - 1)}{2} = \frac{1}{2} > 0.\]
\[f(5) = \frac{1^{2}\left( 2 + \log_{\frac{1}{3}}5 \right)}{5 - 1} = \frac{2 - \log_{3}5}{4} > 0.\]
\[f(27) = \frac{23^{2}\left( 2 + \log_{\frac{1}{3}}27 \right)}{27 - 1} = \frac{23^{2} \cdot (2 - 3)}{26} = - \frac{529}{26} < 0.\]

\[x \in (0;1) \cup \left\{ 4 \right\} \cup \lbrack 9; + \infty).\]
\[Ответ:x \in (0;1) \cup \left\{ 4 \right\} \cup \lbrack 9; + \infty).\]
\[\textbf{г)}\ \frac{\left( x^{2} - 11x + 10 \right)\left( \lg x - 1 \right)}{\left( 2^{x} - 2 \right)^{2}} \leq 0\]
\[1)\ \left( 2^{x} - 2 \right)^{2} \neq 0\]
\[2^{x} \neq 2\]
\[x \neq 1.\]
\[x > 0.\]
\[2)\ x^{2} - 11x + 10 = 0\]
\[x_{1} + x_{2} = 11;\ \ x_{1} \cdot x_{2} = 10\]
\[x_{1} = 1;\ \ \ x_{2} = 10.\]
\[\lg x - 1 = 0\]
\[\lg x = 1\]
\[x = 10.\]
\[M = (0;1) \cup (1;10) \cup (10; + \infty).\]
\[3)\ f\left( \frac{1}{2} \right) = \frac{\left( \frac{1}{4} - \frac{22}{4} + 10 \right)\left( \lg\frac{1}{2} - \lg 10 \right)}{\left( 2^{\frac{1}{2}} - 2 \right)^{2}} = \frac{\frac{19}{4} \cdot \lg\frac{1}{20}}{\left( \sqrt{2} - 2 \right)^{2}} < 0.\]
\[f(2) = \frac{(4 - 22 + 10)\left( \lg 2 - \lg 10 \right)}{2^{2}} = \frac{- 8 \cdot \lg\frac{1}{5}}{4} > 0.\]
\[f(11) = \frac{(121 - 121 + 10)\left( \lg 11 - 1 \right)}{\left( 2^{11} - 2 \right)^{2}} = \frac{10 \cdot \left( \lg 11 - \lg 10 \right)}{2046^{2}} = \frac{10 \cdot \lg\frac{11}{10}}{2046^{2}} > 0.\]

\[x \in (0;1) \cup \left\{ 10 \right\}.\]
\[Ответ:x \in (0;1) \cup \left\{ 10 \right\}.\]
\[\boxed{\mathbf{22.}}\]
\[\textbf{а)}\ \frac{2^{x - 1} + 6 \cdot 4^{x} + 1}{3 \cdot 4^{x} - 10 \cdot 2^{x - 1} - 28} \geq - 1\]
\[\frac{\frac{2^{x}}{2} + 6 \cdot 4^{x} + 1}{3 \cdot 4^{x} - 10 \cdot \frac{2^{x}}{2} - 28} + 1 \geq 0\]
\[\frac{0,5 \cdot 2^{x} + 6 \cdot 4^{x} + 1 + 3 \cdot 4^{x} - 5 \cdot 2^{x} - 28}{3 \cdot 4^{x} - 5 \cdot 2^{x} - 28} \geq 0\]
\[\frac{9 \cdot 4^{x} - 4,5 \cdot 2^{x} - 27}{3 \cdot 4^{x} - 5 \cdot 2^{x} - 28} \geq 0\]
\[1)\ 3 \cdot 4^{x} - 5 \cdot 2^{x} - 28 \neq 0\]
\[2^{x} = t:\]
\[3t^{2} - 5t - 28 = 0\]
\[D = 25 + 336 = 361 = 19^{2}\]
\[t_{1} = \frac{5 + 19}{6} = 4;\]
\[t_{2} = \frac{5 - 19}{6} = - \frac{14}{6} = - \frac{7}{3}.\]
\[2^{x} = 4\]
\[2^{x} = 2^{2}\]
\[x = 2.\]
\[2^{x} = - \frac{7}{3}\]
\[нет\ корней.\]
\[x \neq 2.\]
\[2)\ 9 \cdot 4^{x} - 4,5 \cdot 2^{x} - 27 = 0\]
\[2^{x} = y:\]
\[9y^{2} - 4,5y - 27 = 0\ \ \ \ \ |\ :4,5\ \]
\[2y^{2} - y - 6 = 0\]
\[D = 1 + 48 = 49\]
\[y_{1} = \frac{1 + 7}{4} = 2;\]
\[y_{2} = \frac{1 - 7}{4} = - \frac{6}{4} < 0\ (не\ подходит).\]
\[2^{x} = 2\]
\[x = 1.\]
\[M = ( - \infty;1) \cup (1;2) \cup (2; + \infty).\]
\[3)\ f(0) = \frac{9 \cdot 1 - 4,5 \cdot 1 - 27}{3 \cdot 1 - 5 \cdot 1 - 28} = \frac{- 22,5}{- 20} > 0.\]
\[f(\ 1,5) = \frac{9 \cdot 4^{\frac{3}{2}} - 4,5 \cdot 2^{\frac{3}{2}} - 27}{3 \cdot 4^{\frac{3}{2}} - 5 \cdot 2^{\frac{3}{2}} - 28} = \frac{9 \cdot 2^{3} - 4,5\sqrt{8} - 27}{24 - 5\sqrt{8} - 28} = \frac{45 - 4,5\sqrt{8}}{4 - 5\sqrt{8}} < 0.\]
\[f(3) = \frac{9 \cdot 4^{3} - 4,5 \cdot 2^{3} - 27}{3 \cdot 4^{3} - 5 \cdot 2^{3} - 28} = \frac{576 - 36 - 27}{192 - 40 - 28} = \frac{513}{124} > 0.\]

\[x \in ( - \infty;1\rbrack \cup (2; + \infty).\]
\[Ответ:x \in ( - \infty;1\rbrack \cup (2; + \infty).\]
\[\textbf{б)}\ \frac{5 \cdot 2^{x - 1} - 2 \cdot 4^{x} - 26}{3 \cdot 4^{x} - 7 \cdot 2^{x - 1} - 34} \geq 1\]
\[\frac{\frac{5}{2} \cdot 2^{x} - 2 \cdot 4^{x} - 26}{3 \cdot 4^{x} - \frac{7}{2} \cdot 2^{x} - 34} - 1 \geq 0\]

\[\frac{6 \cdot 2^{x} - 5 \cdot 4^{x} + 8}{3 \cdot 4^{x} - 3,5 \cdot 2^{x} - 34} \geq 0\]
\[1)\ 3 \cdot 4^{x} - 3,5 \cdot 2^{x} - 34 \neq 0\]
\[2^{x} = t:\]
\[3t^{2} - 3,5t - 34 = 0\ \ \ | \cdot 2\]
\[6t^{2} - 7t - 68 = 0\]
\[D = 49 + 1632 = 1681 = 41^{2}\]
\[t_{1} = \frac{7 + 41}{12} = 4;\]
\[t_{2} = \frac{7 - 41}{12} = - \frac{34}{12} < 0\ (не\ подходит).\]
\[2^{x} = 4\]
\[2^{x} = 2^{2}\]
\[x \neq 2.\]
\[2)\ 6 \cdot 2^{x} - 5 \cdot 4^{x} + 8 = 0\]
\[5 \cdot 4^{x} - 6 \cdot 2^{x} - 8 = 0\]
\[2^{x} = y:\]
\[5y^{2} - 6y - 8 = 0\]
\[D_{1} = 9 + 40 = 49\]
\[y_{1} = \frac{3 + 7}{5} = 2;\]
\[y_{2} = \frac{3 - 7}{5} = - \frac{4}{5} < 0\ (не\ подходит).\]
\[M = ( - \infty;1) \cup (1;2) \cup (2; + \infty).\]
\[3)\ \]


\[= \frac{\sqrt{288} - \sqrt{1024}}{- 3,5\sqrt{2} - 28} > 0.\]
\[f(3) = \frac{6 \cdot 2^{3} - 5 \cdot 4^{3} + 8}{3 \cdot 4^{3} - 3,5 \cdot 2^{3} - 34} = \frac{48 - 320 + 8}{192 - 28 - 34} = - \frac{264}{130} < 0.\]

\[x \in \lbrack 1;2).\]
\[Ответ:x \in \lbrack 1;2).\]
\[\boxed{\mathbf{23.}}\]
\[\textbf{а)}\ 2^{\sqrt{x^{2} - 9}}(x - 5)\log_{6}{(9 - x)} < 0\]
\[1)\ x^{2} - 9 \geq 0\]
\[(x + 3)(x - 3) \geq 0\]
\[x \leq - 3;\ \ x \geq 3.\]
\[9 - x > 0\]
\[x < 9.\]
\[2)\ 2^{\sqrt{x^{2} - 9}} = 0\]
\[нет\ корней.\]
\[x - 5 = 0\]
\[x = 5.\]
\[\log_{6}(9 - x) = 0\]
\[9 - x = 1\]
\[x = 8.\]
\[M = ( - \infty; - 3\rbrack \cup \lbrack 3;5) \cup (5;8) \cup (8;9).\]
\[3)\ \]





\[x \in ( - \infty; - 3\rbrack \cup \lbrack 3;5) \cup (8;9).\]
\[Ответ:x \in ( - \infty; - 3\rbrack \cup \lbrack 3;5) \cup (8;9).\]
\[\textbf{б)}\ \ 3^{\sqrt{x^{2} - 16}}(6 - x)\log_{2}{(12 + x)} > 0\]
\[1)\ x^{2} - 16 \geq 0\]
\[(x + 4)(x - 4) \geq 0\]
\[x \leq - 4;\ \ x \geq 4.\]
\[12 + x > 0\]
\[x > - 12.\]
\[2)\ 3^{\sqrt{x^{2} - 16}} = 0\]
\[нет\ корней.\]
\[6 - x = 0\]
\[x = 6.\]
\[\log_{2}(12 + x) = 0\]
\[12 + x = 1\]
\[x = - 11.\]
\[M = ( - 12; - 11) \cup ( - 11; - 4\rbrack \cup \lbrack 4;6) \cup (6; + \infty).\]
\(3)\ \)
\[= 3^{\sqrt{116,25}} \cdot 17,5 \cdot \log_{2}{0,5} < 0.\]

\[= 297 \cdot \log_{2}7 > 0.\]



\[x \in ( - 11; - 4\rbrack \cup \lbrack 4;6).\]
\[Ответ:x \in ( - 11; - 4\rbrack \cup \lbrack 4;6).\]
