Решебник по алгебре 11 класс Никольский Параграф 1. Функции и их графики Задание 82

\[\boxed{\mathbf{82.}}\]

\[\textbf{а)}\ y = x|x|\]

\[x \geq 0:\]

\[y = x^{2}.\]

\[x < 0:\]

\[y = - x^{2}.\]

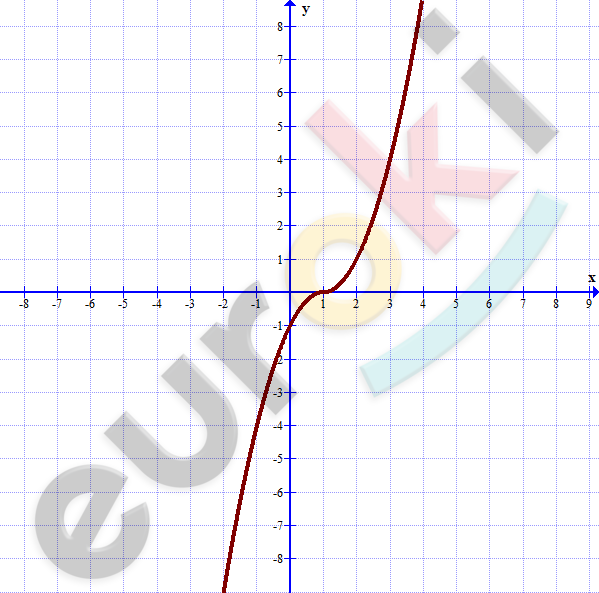
\[\textbf{б)}\ y = (x - 1)|x - 1|\]

\[x \geq 1:\]

\[y = (x - 1)^{2}.\]

\[x < 1:\]

\[y = - (x - 1)^{2}.\]

\[\textbf{в)}\ y = |x||x - 2|\]

\[x \geq 2:\]

\[y = x(x - 2) = x^{2} - 2x.\]

\[x < 0:\]

\[y = - x\left( - (x - 2) \right) = x^{2} - 2x.\]

\[0 \leq x < 2:\]

\[y = x( - (x - 2) = - x^{2} + 2x.\]

\[\textbf{г)}\ y = |x + 2||x - 2|\]

\[x < - 2:\]

\[y = - (x + 2)( - (x - 2) =\]

\[= (x + 2)(x - 2) = x^{2} - 4.\]

\[- 2 \leq x < 2:\]

\[y = (x + 2)\left( - (x - 2) \right) =\]

\[= - (x + 2)(x - 2) = - x^{2} + 4.\]

\[x \geq 2:\]

\[y = (x + 2)(x - 2) = x^{2} - 4.\]

\[\textbf{д)}\ y = (|x| - 1)(|x| + 4)\]

\[x \geq 0:\]

\[y = (x - 1)(x + 4) = x^{2} + 3x - 4.\]

\[x < 0:\]

\[y = ( - x - 1)( - x + 4) =\]

\[= (x + 1)(x - 4) = x^{2} - 3x - 4.\]

\[\textbf{е)}\ y = (|x| - 3)(|x| + 2)\]

\[x \geq 0:\]

\[y = (x - 3)(x + 2) = x^{2} - x - 6.\]

\[x < 0:\]

\[y = ( - x - 3)( - x + 2) = x^{2} +\]

\[+ 3x - 2x - 6 = x^{2} + x - 6.\]