Решебник по алгебре и начала математического анализа 11 класс Колягин Задание 948

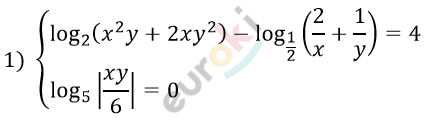
\[\log_{5}\left| \frac{\text{xy}}{6} \right| = 0\]

\[\left| \frac{\text{xy}}{6} \right| = 1\]

\[xy = \pm 6.\]

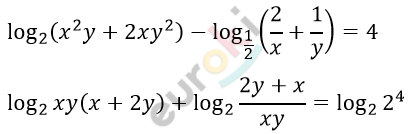
\[\log_{2}(2y + x)^{2} = \log_{2}16\]

\[(x + 2y)^{2} = 16\]

\[x + 2y = \pm 4.\]

\[Область\ определения:\]

\[\frac{2}{x} + \frac{1}{y} > 0\]

\[\frac{2y + x}{\text{xy}} > 0.\ \]

\[x^{2}y + 2xy^{2} > 0\]

\[\text{\ xy}(x + 2y) > 0.\]

\[1)\ x + 2y = - 4\]

\[x = - 4 - 2y.\]

\[xy = - 6\]

\[y( - 4 - 2y) = - 6\]

\[- 4y - 2y^{2} + 6 = 0\]

\[y^{2} + 2y - 3 = 0\]

\[D = 4 + 12 = 16\]

\[y_{1} = \frac{- 2 - 4}{2} = - 3;\]

\[y_{2} = \frac{- 2 + 4}{2} = 1;\]

\[x_{1} = - 4 + 6 = 2;\]

\[x_{2} = - 4 - 2 = - 6.\]

\[2)\ x + 2y = 4\]

\[x = 4 - 2y.\]

\[xy = 6\]

\[y(4 - 2y) = 6\]

\[4y - 2y^{2} - 6 = 0\]

\[y^{2} - 2y + 3 = 0\]

\[D = 4 - 12 = - 8 < 0\]

\[y \in \varnothing.\]

\[Ответ:\ \ (2;\ - 3);\ ( - 6;\ 1).\]

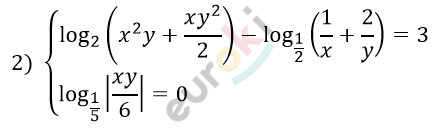
\[\log_{\frac{1}{5}}\left| \frac{\text{xy}}{6} \right| = 0\]

\[\left| \frac{\text{xy}}{6} \right| = 1\]

\[xy = \pm 6.\]

\[\log_{2}\frac{(2x + y)^{2}}{2} = \log_{2}8\]

\[\frac{(2x + y)^{2}}{2} = 8\]

\[(2x + y)^{2} = 16\]

\[2x + y = \pm 4.\]

\[Область\ определения:\]

\[x^{2}y + \frac{xy^{2}}{2} > 0\]

\[\frac{\text{xy}}{2}(2x + y) > 0.\]

\[\frac{1}{x} + \frac{2}{y} > 0\ \ \]

\[\frac{y + 2x}{\text{xy}} > 0.\]

\[1)\ 2x + y = - 4\]

\[y = - 4 - 2x.\]

\[xy = - 6\ \ \ \]

\[x( - 4 - 2x) = - 6\]

\[- 4x - 2x^{2} + 6 = 0\]

\[x^{2} + 2x - 3 = 0\]

\[D = 4 + 12 = 16\]

\[x_{1} = \frac{- 2 - 4}{2} = - 3;\]

\[x_{2} = \frac{- 2 + 4}{2} = 1;\]

\[y_{1} = - 4 + 6 = 2;\]

\[y_{2} = - 4 - 2 = - 6.\]

\[2)\ 2x + y = 4\]

\[y = 4 - 2x.\]

\[xy = 6\]

\[x(4 - 2x) = 6\]

\[4x - 2x^{2} - 6 = 0\]

\[x^{2} - 2x + 3 = 0\]

\[D = 4 - 12 = - 8 < 0\]

\[x \in \varnothing.\]

\[Ответ:\ \ ( - 3;\ 2);\ (1;\ - 6).\]