Решебник по алгебре и начала математического анализа 11 класс Колягин Задание 665

\[1)\ (5 + 3i) + z = - 4 - i\]

\[5 + 3i + z = - 4 - i\]

\[z = - 9 - 4i.\]

\[2)\ ( - 2 + i) + z = 3 - 2i\]

\[- 2 + i + z = 3 - 2i\]

\[z = 5 - 3i.\]

\[3)\ 5 + i = z - \left( 3 - \sqrt{2} \right)i\]

\[5 + i = z - 3i + \sqrt{2}i\]

\[z = 5 + 4i - \sqrt{2}i\]

\[z = 5 + \left( 4 - \sqrt{2} \right)i.\]

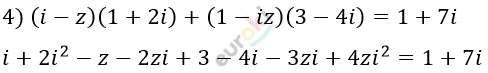
\[z + 5zi - 4zi^{2} = 2 - 10i + 2i^{2}\]

\[z + 5zi + 4z = 2 - 10i - 2\]

\[5z + 5zi = - 10i\]

\[z(5 + 5i) = - 10i\]

\[z = \frac{- 10i}{5 + 5i} = \frac{- 10i(5 - 5i)}{(5 + 5i)(5 - 5i)} =\]

\[= \frac{- 50i + 50i^{2}}{25 - 25i^{2}} = \frac{- 50 - 50i}{25 + 25} =\]

\[= \frac{- 50 - 50i}{50} = - 1 - i.\]