Решебник по алгебре и начала математического анализа 11 класс Колягин Задание 488

\[1)\ C_{12}^{2} + C_{12}^{3} + C_{13}^{4} = C_{13}^{3} + C_{13}^{4} =\]

\[= C_{14}^{4} = \frac{14!}{4!(14 - 4)!} =\]

\[= \frac{14 \bullet 13 \bullet 12 \bullet 11 \bullet 10!}{4 \bullet 3 \bullet 2 \bullet 10!} =\]

\[= 7 \bullet 13 \bullet 11 = 1001;\]

\[2)\ C_{9}^{3} + C_{9}^{4} + C_{10}^{5} = C_{10}^{4} + C_{10}^{5} =\]

\[= C_{11}^{5} = \frac{11!}{5!(11 - 5)!} =\]

\[= \frac{11 \bullet 10 \bullet 9 \bullet 8 \bullet 7 \bullet 6!}{5 \bullet 4 \bullet 3 \bullet 2 \bullet 6!} =\]

\[= 11 \bullet 3 \bullet 2 \bullet 7 = 462;\]

\[3)\ C_{8}^{4} - C_{7}^{4} = C_{7}^{3} + C_{7}^{4} - C_{7}^{4} =\]

\[= C_{7}^{3} = \frac{7!}{3!(7 - 3)!} =\]

\[= \frac{7 \bullet 6 \bullet 5 \bullet 4!}{3 \bullet 2 \bullet 4!} = 7 \bullet 5 = 35;\]

\[4)\ C_{9}^{3} - C_{8}^{2} = C_{8}^{2} + C_{8}^{3} - C_{8}^{2} =\]

\[= C_{8}^{3} = \frac{8!}{3!(8 - 3)!} =\]

\[= \frac{8 \bullet 7 \bullet 6 \bullet 5!}{3 \bullet 2 \bullet 5!} = 8 \bullet 7 = 56;\]

\[5)\ C_{7}^{4} + C_{7}^{5} + C_{7}^{6} + C_{7}^{7} = x\]

\[2^{7} - \left( C_{7}^{7} + C_{7}^{6} + C_{7}^{5} + C_{7}^{4} \right) = x\]

\[2^{7} - x = x\]

\[2x = 2^{7}\]

\[x = 2^{6} = 64.\]

\[Ответ:\ \ 64.\]

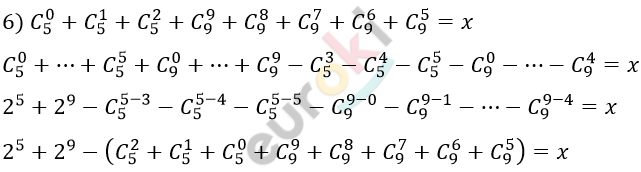
\[2^{5} + 2^{9} - x = x\]

\[2x = 2^{5} + 2^{9}\]

\[x = 2^{4} + 2^{8}\]

\[x = 16 + 256 = 272.\]

\[Ответ:\ \ 272.\]