Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по алгебре и начала математического анализа 11 класс Колягин Задание 47
Задание 47
\[1)\ y = 1 + \cos x\]
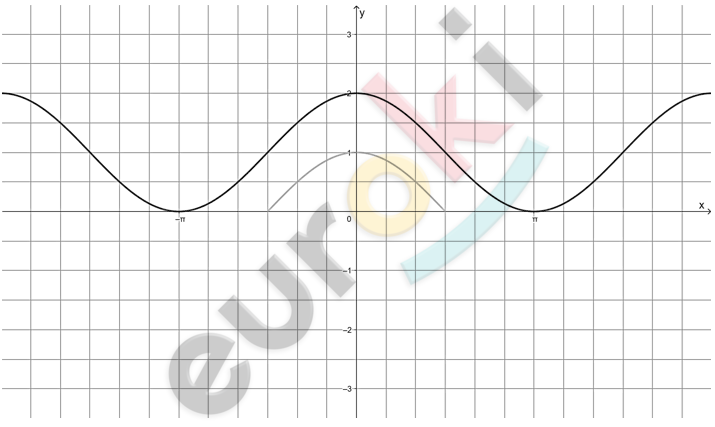
\[1)\ D(x) = ( - \infty;\ + \infty);\ \ \ \]
\[E(y) = \lbrack 0;\ 2\rbrack;\]
\[2)\ Периодическая:\ \ T = 2\pi;\]
\[3)\ Функция\ является\ четной;\]
\[4)\ f(x) > 0\ на\ \]
\[x \in ( - \pi + 2\pi n;\ \pi + 2\pi n);\]
\[5)\ Возрастает\ на\ \lbrack - \pi + 2\pi n;\ 2\pi n\rbrack;\]
\[убывает\ на\ \lbrack 2\pi n;\ \pi + 2\pi n\rbrack.\]
\[2)\ y = \cos{2x}\]
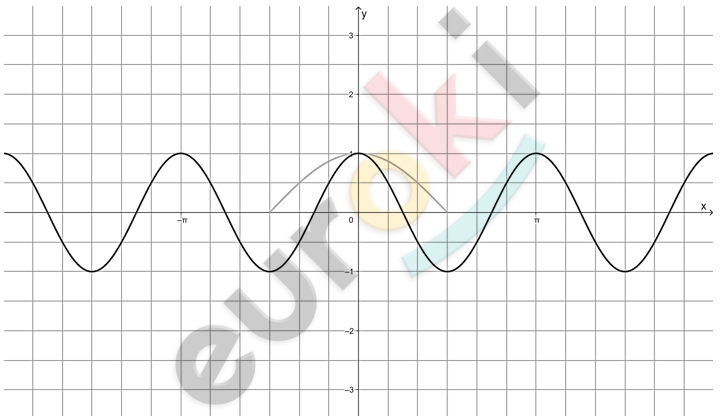
\[1)\ D(x) = ( - \infty;\ + \infty);\ \ \ \]
\[E(y) = \lbrack - 1;\ 1\rbrack;\]
\[2)\ Периодическая:\ \ T = \pi;\]
\[3)\ Функция\ является\ четной;\]
\[4)\ f(x) > 0\ на\ \]
\[x \in \left( - \frac{\pi}{4} + \pi n;\ \frac{\pi}{4} + \pi n \right);\]
\[\text{\ f}(x) < 0\ на\ \]
\[x \in \left( \frac{\pi}{4} + \pi n;\ \frac{3\pi}{4} + \pi n \right);\]
\[5)\ Возрастает\ на\ \left\lbrack - \frac{\pi}{2} + \pi n;\ \text{πn} \right\rbrack;\]
\[убывает\ на\ \left\lbrack \pi n;\ \frac{\pi}{2} + 2\pi n \right\rbrack.\]
\[3)\ y = 3\cos x\]
\[1)\ D(x) = ( - \infty;\ + \infty);\ \ \ \]
\[E(y) = \lbrack - 3;\ 3\rbrack;\]
\[2)\ Периодическая:\ \ T = 2\pi;\]
\[3)\ Функция\ является\ четной;\]
\[4)\ f(x) > 0\ на\ \]
\[x \in \left( - \frac{\pi}{2} + 2\pi n;\ \frac{\pi}{2} + 2\pi n \right);\]
\[f(x) < 0\ на\ \]
\[x \in \left( \frac{\pi}{2} + 2\pi n;\ \frac{3\pi}{2} + 2\pi n \right);\]
\[5)\ Возрастает\ на\ \left\lbrack - \pi + 2\pi n;\ 2\text{πn} \right\rbrack;\]
\[убывает\ на\ \lbrack 2\pi n;\ \pi + 2\pi n\rbrack.\]
\[4)\ y = 2\cos\frac{x}{2}\]
\[1)\ D(x) = ( - \infty;\ + \infty);\ \ \ \]
\[E(y) = \lbrack - 2;\ 2\rbrack;\]
\[2)\ Периодическая:\ \ T = 4\pi;\]
\[3)\ Функция\ является\ четной;\]
\[4)\ f(x) > 0\ на\ \]
\[x \in ( - \pi + 4\pi n;\ \pi + 4\pi n);\]
\[f(x) < 0\ на\ \]
\[x \in (\pi + 4\pi n;\ 3\pi + 4\pi n);\]
\[5)\ Возрастает\ на\ \left\lbrack - 2\pi + 4\pi n;\ 4\text{πn} \right\rbrack;\]
\[убывает\ на\ \lbrack 4\pi n;\ 2\pi + 4\pi n\rbrack.\]
\[5)\ y = \frac{\cos{2x}}{2} - 1\]
\[1)\ D(x) = ( - \infty;\ + \infty);\ \]
\[E(y) = \lbrack - 1,5;\ - 0,5\rbrack;\]
\[2)\ Периодическая:\ \ T = \pi;\]
\[3)\ Функция\ является\ четной;\]
\[4)\ f(x) < 0\ на\ x \in ( - \infty;\ + \infty);\]
\[5)\ Возрастает\ на\ \left\lbrack - \frac{\pi}{2} + \pi n;\ \text{πn} \right\rbrack;\]
\[убывает\ на\ \left\lbrack \pi n;\ \frac{\pi}{2} + \pi n \right\rbrack.\]
\[6)\ y = 2 - \cos{3x}\]
\[1)\ D(x) = ( - \infty;\ + \infty);\ \ \ \]
\[E(y) = \lbrack 1;\ 3\rbrack;\]
\[2)\ Периодическая:\ \ T = \frac{2\pi}{3};\]
\[3)\ Функция\ является\ четной;\]
\[4)\ f(x) > 0\ на\ x \in ( - \infty;\ + \infty);\]
\[5)\ Возрастает\ на\ \left\lbrack \frac{2\pi n}{3};\ \frac{\pi}{3} + \frac{2\pi n}{3} \right\rbrack;\]
\[убывает\ на\ \left\lbrack - \frac{\pi}{3} + \frac{2\pi n}{3};\ \frac{2\pi n}{3} \right\rbrack.\]
