Решебник по алгебре и начала математического анализа 11 класс Колягин Задание 371

\[1)\ \int_{- 2}^{1}{x(x + 3)(2x - 1)\text{dx}} =\]

\[= \int_{- 2}^{1}{\left( x^{2} + 3x \right)(2x - 1)\text{dx}} =\]

\[= \int_{- 2}^{1}{\left( 2x^{3} + 5x^{2} - 3x \right)\text{dx}} =\]

\[= \left. \ \left( \frac{1}{2}x^{4} + \frac{5}{3}x^{3} - \frac{3}{2}x^{2} \right) \right|_{- 2}^{1} =\]

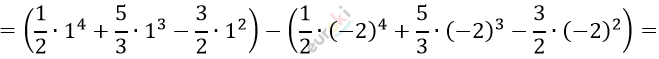
\[= \left( \frac{1}{2} + \frac{5}{3} - \frac{3}{2} \right) - \left( \frac{16}{2} - \frac{40}{3} - \frac{12}{2} \right) =\]

\[= - \frac{6}{2} + \frac{45}{3} = - 3 + 15 = 12.\]

\[2)\ \int_{1}^{2}{\left( x + \frac{1}{x} \right)^{2}\text{dx}} =\]

\[= \int_{1}^{2}{\left( x^{2} + 2 + \frac{1}{x^{2}} \right)\text{dx}} =\]

\[= \left. \ \left( \frac{x^{3}}{3} + 2x + \frac{x^{- 1}}{- 1} \right) \right|_{1}^{2} =\]

\[= \left( \frac{8}{3} + 4 - \frac{1}{2} \right) - \left( \frac{1}{3} + 2 - 1 \right) =\]

\[= \frac{7}{3} - \frac{1}{2} + 3 = \frac{14 - 3}{6} + 3 =\]

\[= \frac{11}{6} + 3 = 1\frac{5}{6} + 3 = 4\frac{5}{6}.\]

\[3)\ \int_{- 1}^{0}{(x + 1)\left( x^{2} - 2 \right)\text{dx}} =\]

\[= \int_{- 1}^{0}{\left( x^{3} + x^{2} - 2x - 2 \right)\text{dx}} =\]

\[= \left. \ \left( \frac{x^{4}}{4} + \frac{x^{3}}{3} - x^{2} - 2x \right) \right|_{- 1}^{0} =\]

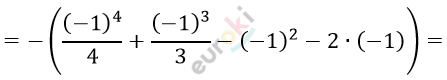
\[= - \left( \frac{1}{4} - \frac{1}{3} - 1 + 2 \right) =\]

\[= - \left( \frac{3 - 4}{12} + 1 \right) = \frac{1}{12} - 1 = - \frac{11}{12}.\]

\[4)\ \int_{- 2}^{- 1}{\frac{4}{x^{2}}\left( 1 - \frac{2}{x} \right)\text{dx}} =\]

\[= \int_{- 2}^{- 1}{\left( \frac{4}{x^{2}} - \frac{8}{x^{3}} \right)\text{dx}} =\]

\[= \left. \ \left( 4 \bullet \frac{x^{- 1}}{- 1} - 8 \bullet \frac{x^{- 2}}{- 2} \right) \right|_{- 2}^{- 1} =\]

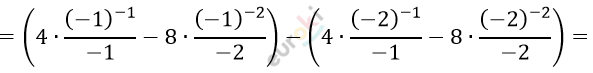
\[= (4 + 4) - \left( 4 \bullet \frac{1}{2} + 4 \bullet \frac{1}{4} \right) =\]

\[= 8 - 2 - 1 = 8 - 3 = 5.\]