Решебник по алгебре и начала математического анализа 11 класс Колягин Задание 361

\[1)\ f(x) = e^{3x} - \cos{2x};\]

\[F(x) = \frac{1}{3}e^{3x} - \frac{1}{2}\sin{2x} + C.\]

\[2)\ f(x) = e^{\frac{x}{3}} + \sin{3x};\]

\[F(x) = 3e^{\frac{x}{3}} - \frac{1}{3}\cos{3x} + C.\]

\[3)\ f(x) = 2\sin\frac{x}{3} - 5e^{2x + \frac{1}{5}};\]

\[F(x) =\]

\[= 2 \bullet \left( - 3\cos\frac{x}{3} \right) - 5 \bullet \frac{1}{2}e^{2x + \frac{1}{5}} + C =\]

\[= - 6\cos\frac{x}{3} - \frac{5}{2}e^{2x + \frac{1}{5}} + C.\]

\[4)\ f(x) = 3\cos\frac{x}{7} + 2e^{3x - \frac{1}{2}};\]

\[F(x) =\]

\[= 3 \bullet 7\sin\frac{x}{7} + 2 \bullet \frac{1}{3}e^{3x - \frac{1}{2}} + C =\]

\[= 21\sin\frac{x}{7} + \frac{2}{3}e^{3x - \frac{1}{2}} + C.\]

\[5)\ f(x) = \sqrt[5]{\frac{x}{4}} - 5\cos(6x - 1);\]

\[F(x) =\]

\[= 4 \bullet \left( \frac{x}{4} \right)^{\frac{6}{5}}\ :\frac{6}{5} - 5 \bullet \frac{1}{6}\sin(6x - 1) + C =\]

\[= \frac{10}{3} \bullet \left( \frac{x}{4} \right)^{\frac{6}{5}} - \frac{5}{6}\sin(6x - 1) + C.\]

\[6)\ f(x) = \sqrt{\frac{x}{5}} + 4\sin(4x + 2);\]

\[F(x) =\]

\[= 5 \bullet \left( \frac{x}{5} \right)^{\frac{3}{2}}\ :\frac{3}{2} - 4 \bullet \frac{1}{4}\cos(4x + 2) + C =\]

\[= \frac{10}{3} \bullet \left( \frac{x}{5} \right)^{\frac{3}{2}} - \cos(4x + 2) + C.\]

\[7)\ f(x) = \frac{3}{\sqrt[3]{2x - 1}};\]

\[F(x) = 3 \bullet \frac{1}{2} \bullet (2x - 1)^{\frac{2}{3}}\ :\frac{2}{3} + C =\]

\[= \frac{9}{4}(2x - 1)^{\frac{2}{3}} + C.\]

\[8)\ f(x) = \frac{4}{\sqrt{3x + 1}} - \frac{3}{2x - 5};\]

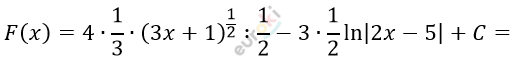
\[= \frac{8}{3}\sqrt{3x + 1} - \frac{3}{2}\ln|2x - 5| + C.\]