Решебник по алгебре и начала математического анализа 11 класс Колягин Задание 157

\[1)\ f(x) = 2x + 3;\]

\[f^{'}(x) =\]

\[= \lim_{h \rightarrow 0}\frac{\left( 2(x + h) + 3 \right) - (2x + 3)}{h} =\]

\[= \lim_{h \rightarrow 0}\frac{2x + 2h - 2x}{h} = \lim_{h \rightarrow 0}\frac{2h}{h} =\]

\[= \lim_{h \rightarrow 0}2 = 2.\]

\[Ответ:\ \ 2.\]

\[2)\ f(x) = 5x - 6;\]

\[f^{'}(x) =\]

\[= \lim_{h \rightarrow 0}\frac{\left( 5(x + h) - 6 \right) - (5x - 6)}{h} =\]

\[= \lim_{h \rightarrow 0}\frac{5x + 5h - 5x}{h} = \lim_{h \rightarrow 0}\frac{5h}{h} =\]

\[= \lim_{h \rightarrow 0}5 = 5.\]

\[Ответ:\ \ 5.\]

\[3)\ f(x) = - 3x^{2} + 2;\]

\[f^{'}(x) =\]

\[= \lim_{h \rightarrow 0}\frac{\left( - 3(x + h)^{2} + 2 \right) - \left( - 3x^{2} + 2 \right)}{h} =\]

\[= \lim_{h \rightarrow 0}\frac{- 3x^{2} - 6xh - 3h^{2} + 3x^{2}}{h} =\]

\[= \lim_{h \rightarrow 0}\frac{- 6xh - 3h^{2}}{h} =\]

\[= \lim_{h \rightarrow 0}( - 6x - 3h) = - 6x.\]

\[Ответ:\ - 6x.\]

\[4)\ f(x) = 3x^{2} + 5x;\]

\[f^{'}(x) =\]

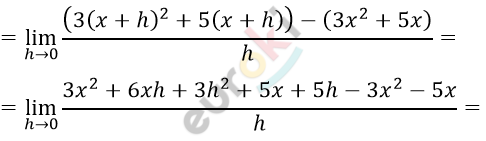
\[= \lim_{h \rightarrow 0}\frac{6xh + 3h^{2} + 5h}{h} =\]

\[= \lim_{h \rightarrow 0}(6x + 3h + 5) = 6x + 5.\]

\[Ответ:\ \ 6x + 5.\]