Решебник по алгебре и начала математического анализа 11 класс Колягин Задание 1095

\[r - радиус\ основания;\]

\[h - высота\ цилиндра:\]

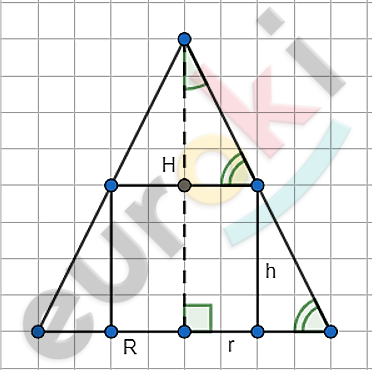
\[1)\ Из\ подобия\ \mathrm{\Delta}:\]

\[\frac{h}{H} = \frac{(R - r)}{R}\]

\[h = \frac{H(R - r)}{R}.\]

\[2)\ Объем\ цилиндра:\]

\[V(r) = \pi r^{2}h = \pi r^{2} \bullet \frac{H(R - r)}{R} =\]

\[= \frac{\text{HRπ}r^{2} - H\pi r^{3}}{R}.\]

\[3)\ V^{'}(r) = \frac{\text{Hπ}}{R} \bullet \left( R\left( r^{2} \right)^{'} - \left( r^{3} \right)^{'} \right) =\]

\[= \frac{\text{Hπ}}{R}\left( 2Rr - 3r^{2} \right).\]

\[4)\ Промежуток\ возрастания:\]

\[2Rr - 3r^{2} \geq 0\]

\[r(2R - 3r) \geq 0\]

\[r(3r - 2R) \leq 0\]

\[0 \leq r \leq \frac{2R}{3}.\]

\[5)\ Точка\ максимума:\]

\[h = \frac{H\left( R - \frac{2R}{3} \right)}{R} = \frac{H}{R} \bullet \frac{R}{3} = \frac{H}{3}.\]

\[Ответ:\ \ r = \frac{2R}{3};\ h = \frac{H}{3}.\]