Решебник по алгебре и начала математического анализа 11 класс Алимов Задание 81

\[\boxed{\mathbf{81}\mathbf{.}}\]

\[1)\ \left( 1 - 2\sqrt{\frac{b}{a}} + \frac{b}{a} \right):\left( a^{\frac{1}{2}} - b^{\frac{1}{2}} \right)^{2} =\]

\[= \left( 1 - \left( \frac{b}{a} \right)^{\frac{1}{2}} \right)^{2}:\left( a^{\frac{1}{2}} - b^{\frac{1}{2}} \right)^{2} =\]

\[= \left( \frac{a^{\frac{1}{2}} - b^{\frac{1}{2}}}{a^{\frac{1}{2}}} \right)^{2}:\left( a^{\frac{1}{2}} - b^{\frac{1}{2}} \right)^{2} =\]

\[= \left( \frac{1}{a^{\frac{1}{2}}} \right)^{2} = \frac{1}{a}\]

\[2)\ \left( a^{\frac{1}{3}} + b^{\frac{1}{3}} \right):\left( 2 + \sqrt[3]{\frac{a}{b}} + \sqrt[3]{\frac{b}{a}} \right) =\]

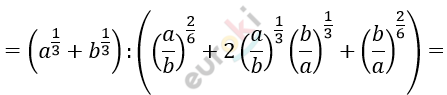
\[= \left( a^{\frac{1}{3}} + b^{\frac{1}{3}} \right):\left( \left( \frac{a}{b} \right)^{\frac{1}{6}} + \left( \frac{b}{a} \right)^{\frac{1}{6}} \right)^{2} =\]

\[= \left( a^{\frac{1}{3}} + b^{\frac{1}{3}} \right):\left( \frac{a^{\frac{2}{6}} + b^{\frac{2}{6}}}{b^{\frac{1}{6}}a^{\frac{1}{6}}} \right)^{2} =\]

\[= \left( a^{\frac{1}{3}} + b^{\frac{1}{3}} \right) \bullet \left( \frac{a^{\frac{1}{6}}b^{\frac{1}{6}}}{a^{\frac{1}{3}} + b^{\frac{1}{3}}} \right)^{2} =\]

\[= \frac{\left( a^{\frac{1}{6}}b^{\frac{1}{6}} \right)^{2}}{a^{\frac{1}{3}} + b^{\frac{1}{3}}} = \frac{a^{\frac{1}{3}}b^{\frac{1}{3}}}{a^{\frac{1}{3}} + b^{\frac{1}{3}}} =\]

\[= \frac{\sqrt[3]{\text{ab}}}{\sqrt[3]{a} + \sqrt[3]{b}}\]

\[3)\ \frac{a^{\frac{1}{4}} - a^{\frac{9}{4}}}{a^{\frac{1}{4}} - a^{\frac{5}{4}}} - \frac{b^{- \frac{1}{2}} - b^{\frac{3}{2}}}{b^{\frac{1}{2}} + b^{- \frac{1}{2}}} =\]

\[= \frac{a^{\frac{1}{4}} \bullet \left( 1 - a^{\frac{8}{4}} \right)}{a^{\frac{1}{4}} \bullet \left( 1 - a^{\frac{4}{4}} \right)} - \frac{b^{- \frac{1}{2}} \bullet \left( 1 - b^{\frac{4}{2}} \right)}{b^{- \frac{1}{2}} \bullet \left( b^{\frac{2}{2}} + 1 \right)} =\]

\[= \frac{1 - a^{2}}{1 - a} - \frac{1 - b^{2}}{1 + b} =\]

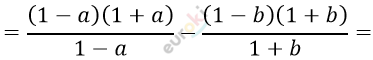
\[= (1 + a) - (1 - b) =\]

\[= 1 + a - 1 + b = a + b\]

\[4)\ \frac{\sqrt{a} - a^{- \frac{1}{2}}b}{1 - \sqrt{a^{- 1}b}} - \frac{\sqrt[3]{a^{2}} - a^{- \frac{1}{3}}b}{\sqrt[6]{a} + a^{- \frac{1}{3}}\sqrt{b}} =\]

\[= \frac{a^{\frac{1}{2}} - a^{- \frac{1}{2}}b}{a^{0} - a^{- \frac{1}{2}}b^{\frac{1}{2}}} - \frac{a^{\frac{2}{3}} - a^{- \frac{1}{3}}b}{a^{\frac{1}{6}} + a^{- \frac{1}{3}}b^{\frac{1}{2}}} =\]

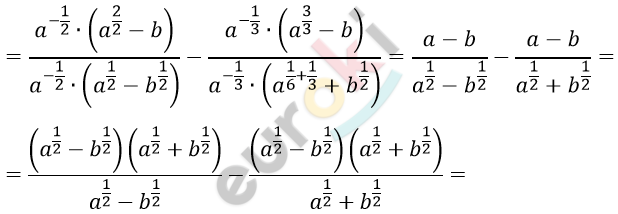
\[= \left( a^{\frac{1}{2}} + b^{\frac{1}{2}} \right) - \left( a^{\frac{1}{2}} - b^{\frac{1}{2}} \right) =\]

\[= a^{\frac{1}{2}} + b^{\frac{1}{2}} - a^{\frac{1}{2}} + b^{\frac{1}{2}} = 2b^{\frac{1}{2}} =\]

\[= 2\sqrt{b}\]