Решебник по алгебре и начала математического анализа 11 класс Алимов Задание 536

\[\boxed{\mathbf{536}\mathbf{.}}\]

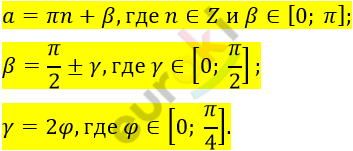
\[1)\ n - четное:\]

\[\sin a = \sin(\pi n + \beta) = \sin\beta\]

\[\cos a = \cos(\pi n + \beta) = \cos\beta\]

\[2)\ n - нечетное:\]

\[\sin a = \sin(\pi n + \beta) = - \sin\beta\]

\[\cos a = \cos(\pi n + \beta) = - \cos\beta\]

\[3)\ Получаем:\]

\[\sin a = \pm \sin\beta =\]

\[= \pm \sin\left( \frac{\pi}{2} \pm \gamma \right) = \pm \cos\gamma\]

\[\cos a = \pm \cos\beta =\]

\[= \pm \cos\left( \frac{\pi}{2} \pm \gamma \right) = \pm \sin( \pm \gamma) =\]

\[= \mp \sin\gamma\]

\[4)\ Формулы\ двойного\ угла:\]

\[\cos\gamma = \cos{2\varphi} = \cos^{2}\varphi - \sin^{2}\varphi\]

\[\sin\gamma = \sin{2\varphi} = 2 \bullet \sin\varphi \bullet \cos\varphi\]

\[5)\ Получаем:\]

\[tg\ a = \frac{\sin a}{\cos a}\text{\ \ }и\ \ ctg\ a = \frac{\cos a}{\sin a}\]

\[Следовательно,\ вычисление\ \]

\[значения\ тригонометрической\ \]

\[функции\ для\ любого\ угла,\ \]

\[сводится\ к\ вычислению\ ее\ \]

\[значения\ для\ угла,\]

\[заключенного\ в\ промежутке\ \]

\[от\ 0\ до\ \frac{\pi}{4}.\]

\[Что\ и\ требовалось\ доказать.\]