Решебник по алгебре и начала математического анализа 11 класс Алимов Задание 1278

\[\boxed{\mathbf{1278}\mathbf{.}}\]

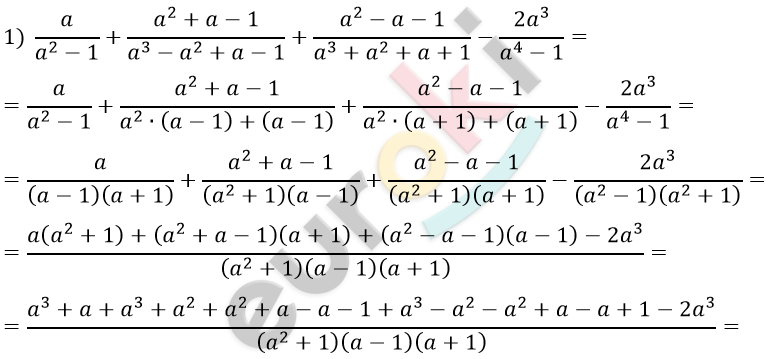
\[= \frac{a^{3} + a}{\left( a^{2} + 1 \right)\left( a^{2} - 1 \right)} =\]

\[= \frac{a \bullet \left( a^{2} + 1 \right)}{\left( a^{2} + 1 \right)\left( a^{2} - 1 \right)} = \frac{a}{a^{2} - 1}\]

\[a^{2} + 5a + 6 = 0\]

\[D = 25 - 24 = 1\]

\[a_{1} = \frac{- 5 - 1}{2} = - 3;\]

\[a_{2} = \frac{- 5 + 1}{2} = - 2;\]

\[(a + 3)(a + 2) = 0.\]

\[a^{2} + 4a + 3 = 0\]

\[D = 16 - 12 = 4\]

\[a_{1} = \frac{- 4 - 2}{2} = - 3;\]

\[a_{2} = \frac{- 4 + 2}{2} = - 1;\]

\[(a + 3)(a + 1) = 0.\]

\[(a + 1)^{2} + a + 1 =\]

\[= a^{2} + 2a + 1 + a + 1 =\]

\[= a^{2} + 3a + 2 = 0\]

\[D = 9 - 8 = 1\]

\[a_{1} = \frac{- 3 - 1}{2} = - 2;\]

\[a_{2} = \frac{- 3 + 1}{2} = - 1;\]

\[(a + 2)(a + 1) = 0.\]

\[= \frac{0}{(a + 1)(a + 2)(a + 3)} = 0.\]