Решебник по алгебре и начала математического анализа 11 класс Алимов Задание 1223

\[\boxed{\mathbf{1223}\mathbf{.}}\]

\[1)\mathbf{\ Дисперсия\ }\]

\[\mathbf{производительности\ труда\ }\]

\[\mathbf{первого\ рабочего:}\]

\[\overline{X} = \frac{8 + 11 + 9 + 12 + 10}{5} =\]

\[= \frac{50}{5} = 10;\]

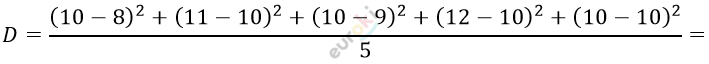
\[= \frac{2^{2} + 1^{2} + 1^{2} + 2^{2} + 0^{2}}{5} =\]

\[= \frac{4 + 1 + 1 + 4}{5} = \frac{10}{5} = 2.\]

\[Дисперсия\ \]

\[производительности\ труда\ \]

\[второго\ рабочего:\]

\[\overline{X} = \frac{8 + 12 + 11 + 8 + 12 + 9}{6} =\]

\[= \frac{60}{6} = 10;\]

\[= \frac{2^{2} + 2^{2} + 1^{2} + 2^{2} + 2^{2} + 1^{2}}{6} =\]

\[= \frac{4 + 4 + 1 + 4 + 4 + 1}{6} = \frac{18}{6} =\]

\[= 3.\]

\[Дисперсия\ произодительности\ \]

\[труда\ первого\ рабочего\ \]

\[меньше,\ значит,его\ \]

\[результаты\ более\ стабильные.\]

\[Ответ:\ \ первый\ рабочий\ \]

\[работает\ более\ стабильно.\]

\[2)\ \mathbf{Дисперсия\ }\]

\[\mathbf{производительности\ труда\ }\]

\[\mathbf{первого\ рабочего:}\]

\[\overline{X} = \frac{9 + 11 + 10 + 11 + 9}{5} =\]

\[= \frac{50}{5} = 10;\]

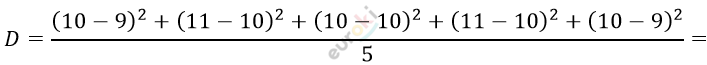
\[= \frac{1^{2} + 1^{2} + 0^{2} + 1^{2} + 1^{2}}{5} =\]

\[= \frac{1 + 1 + 1 + 1}{5} = \frac{4}{5} = 0,8.\]

\[Дисперсия\ \]

\[производительности\ труда\ \]

\[второго\ рабочего:\]

\[\overline{X} =\]

\[= \frac{9 + 10 + 11 + 11 + 10 + 9}{6} =\]

\[= \frac{60}{6} = 10;\]

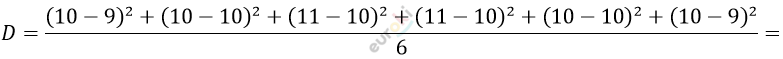
\[= \frac{1^{2} + 0^{2} + 1^{2} + 1^{2} + 0^{2} + 1^{2}}{6} =\]

\[= \frac{4}{6} = \frac{2}{3} = 0,(6).\]

\[Дисперсия\ произодительности\ \]

\[труда\ второго\ рабочего\ \]

\[меньше,\ значит,его\ \]

\[результаты\ более\ стабильные.\]

\[Ответ:\ \ второй\ рабочий\ \]

\[работает\ более\ стабильно.\]