Решебник по алгебре и начала математического анализа 11 класс Алимов Задание 11

\[\boxed{\mathbf{11}\mathbf{.}}\]

\[1)\ \sqrt{3,9} + \sqrt{8}\text{\ \ }и\ \ \sqrt{1,1} + \sqrt{17};\]

\[Границы\ первого\ числа:\]

\[1 < 3,9 < 4\ \ \Longrightarrow 1 < \sqrt{3,9} < 2;\]

\[4 < 8 < 9\ \Longrightarrow 2 < \sqrt{8} < 3;\]

\[3 < \sqrt{3,9} + \sqrt{8} < 5;\]

\[Границы\ второго\ числа:\]

\[1 < 1,1 < 4\ \Longrightarrow 1 < \sqrt{1,1} < 2;\]

\[16 < 17 < 25 \Longrightarrow \ \ \ 4 < \sqrt{17} < 5;\]

\[5 < \sqrt{1,1} + \sqrt{17} < 7;\]

\[Ответ:\ \ \]

\[\sqrt{3,9} + \sqrt{8} < \sqrt{1,1} + \sqrt{17}.\]

\[2)\ \sqrt{11} - \sqrt{2,1}\text{\ \ }и\ \ \sqrt{10} - \sqrt{3,1};\]

\[Допустим,\ что\ верно:\]

\[\sqrt{11} - \sqrt{2,1} > \sqrt{10} - \sqrt{3,1};\]

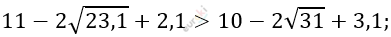
\[13,1 - 2\sqrt{23,1} > 13,1 - 2\sqrt{31};\]

\[- 2\sqrt{23,1} > - 2\sqrt{31};\]

\[\sqrt{23,1} < \sqrt{31};\]

\[23,1 < 31 - верно;\]

\[Ответ:\ \ \]

\[\sqrt{11} - \sqrt{2,1} > \sqrt{10} - \sqrt{3,1}.\]