Решебник по алгебре и начала математического анализа 11 класс Алимов Задание 1091

\[\boxed{\mathbf{1091}\mathbf{.}}\]

\[1)\ C_{x + 1}^{2} + C_{x + 1}^{3} = 7x\]

\[C_{x + 2}^{3} = 7x\]

\[\frac{(x + 2)!}{(x + 2 - 3)! \bullet 3!} = 7x\]

\[\frac{(x + 2) \bullet (x + 1) \bullet x \bullet (x - 1)!}{(x - 1)! \bullet 3 \bullet 2} =\]

\[= 7x\]

\[\frac{(x^{2} + x + 2x + 2) \bullet x}{6} - 7x = 0\]

\[x^{3} + 3x^{2} + 2x - 42x = 0\]

\[x^{3} + 3x^{2} - 40x = 0\]

\[x \bullet \left( x^{2} + 3x - 40 \right) = 0\]

\[D = 3^{2} + 4 \bullet 40 = 9 + 160 = 169\]

\[x_{1} = \frac{- 3 - 13}{2} = - 8\ \ и\ \ \]

\[x_{2} = \frac{- 3 + 13}{2} = 5.\]

\[Ответ:\ \ x = 5.\]

\[2)\ C_{x - 1}^{3} + C_{x - 1}^{2} = 4(x - 1)\]

\[C_{x}^{3} = 4(x - 1)\]

\[\frac{x!}{(x - 3)! \bullet 3!} = 4(x - 1)\]

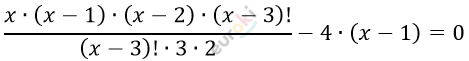
\[\frac{x(x - 2)}{6} - 4 = 0\]

\[x^{2} - 2x - 24 = 0\]

\[D = 2^{2} + 4 \bullet 24 = 4 + 96 = 100\]

\[x_{1} = \frac{2 - 10}{2} = - 4\ \ и\ \ \]

\[x_{2} = \frac{2 + 10}{2} = 6.\]

\[Ответ:\ \ x = 6.\]

\[3)\ C_{x}^{3} = \frac{4}{15} \bullet C_{x + 2}^{4}\]

\[\frac{x!}{(x - 3)! \bullet 3!} =\]

\[= \frac{4}{15} \bullet \frac{(x + 2)!}{(x + 2 - 4)! \bullet 4!}\]

\[\frac{x \bullet (x - 1) \bullet (x - 2) \bullet (x - 3)!}{(x - 3)! \bullet 3 \bullet 2} =\]

\[\frac{x - 2}{6} = \frac{4}{15} \bullet \frac{(x + 2) \bullet (x + 1)}{24}\]

\[x - 2 = \frac{1}{15} \bullet \left( x^{2} + 2x + x + 2 \right)\]

\[15x - 30 = x^{2} + 3x + 2\]

\[x^{2} - 12x + 32 = 0\]

\[D = 12^{2} - 4 \bullet 32 = 144 - 128 =\]

\[= 16\]

\[x_{1} = \frac{12 - 4}{2} = 4\ \ и\ \ \]

\[x_{2} = \frac{12 + 4}{2} = 8.\]

\[Ответ:\ \ x_{1} = 4;\ \ x_{2} = 8.\]

\[4)\ 5 \bullet C_{x}^{3} = C_{x + 2}^{4}\]

\[5 \bullet \frac{x!}{(x - 3)! \bullet 3!} = \frac{(x + 2)!}{(x + 2 - 4)! \bullet 4!}\]

\[\frac{5 \bullet x \bullet (x - 1) \bullet (x - 2) \bullet (x - 3)!}{(x - 3)! \bullet 3 \bullet 2} =\]

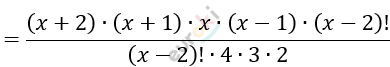
\[\frac{5 \bullet (x - 2)}{6} = \frac{(x + 2)(x + 1)}{24}\]

\[20(x - 2) = x^{2} + 2x + x + 2\]

\[20x - 40 = x^{2} + 3x + 2\]

\[x^{2} - 17x + 42 = 0\]

\[D = 17^{2} - 4 \bullet 42 = 289 - 168 =\]

\[= 121\]

\[x_{1} = \frac{17 - 11}{2} = 3\ \ и\ \]

\[x_{2} = \frac{17 + 11}{2} = 14.\]

\[Ответ:\ \ x_{1} = 3;\ \ x_{2} = 14.\]

\[5)\ C_{3x + 1}^{3x - 1} = 120\]

\[\frac{(3x + 1)!}{(3x + 1 - 3x + 1)! \bullet (3x - 1)!} =\]

\[= 120\]

\[\frac{(3x + 1) \bullet 3x \bullet (3x - 1)!}{2! \bullet (3x - 1)!} - 120 =\]

\[= 0\]

\[\frac{(3x + 1) \bullet 3x}{2} - 120 = 0\]

\[9x^{2} + 3x - 240 = 0\]

\[3x^{2} + x - 80 = 0\]

\[D = 1^{2} + 4 \bullet 3 \bullet 80 = 1 + 960 =\]

\[= 961\]

\[x_{1} = \frac{- 1 - 31}{2 \bullet 3} = - \frac{32}{6}\text{\ \ }\]

\[x_{2} = \frac{- 1 + 31}{2 \bullet 3} = \frac{30}{6} = 5.\]

\[Ответ:\ \ x = 5.\]

\[6)\ C_{2x + 1}^{2x - 1} = 36\]

\[\frac{(2x + 1)!}{(2x + 1 - 2x + 1)! \bullet (2x - 1)!} =\]

\[= 36\]

\[\frac{(2x + 1) \bullet 2x \bullet (2x - 1)!}{2! \bullet (2x - 1)!} - 36 =\]

\[= 0\]

\[\frac{(2x + 1) \bullet 2x}{2} - 36 = 0\]

\[4x^{2} + 2x - 72 = 0\]

\[2x^{2} + x - 36 = 0\]

\[D = 1^{2} + 4 \bullet 2 \bullet 36 = 1 + 288 =\]

\[= 289\]

\[x_{1} = \frac{- 1 - 17}{2 \bullet 2} = - \frac{18}{4}\text{\ \ }\]

\[x_{2} = \frac{- 1 + 17}{2 \bullet 2} = \frac{16}{4} = 4.\]

\[Ответ:\ \ x = 4.\]