Решебник по алгебре и начала математического анализа 10 класс Алимов Задание 1133

\[\boxed{\mathbf{1133}\mathbf{.}}\]

\[n = C_{28}^{2} = \frac{28!}{(28 - 2)! \bullet 2!} =\]

\[= \frac{28!}{26! \bullet 2} = \frac{28 \bullet 27 \bullet 26!}{26! \bullet 2} =\]

\[= 14 \bullet 27 = 378.\]

\[1)\ обе\ костяшки\ окажутся\ \]

\[дублями:\]

\[m = C_{7}^{2} = \frac{7!}{(7 - 2)! \bullet 2!} = \frac{7!}{5! \bullet 2} =\]

\[= \frac{7 \bullet 6 \bullet 5!}{5! \bullet 2} = 7 \bullet 3 = 21;\]

\[P = \frac{m}{n} = \frac{21}{378} = \frac{7}{126} = \frac{1}{18}\text{.\ }\]

\[2)\ на\ каждой\ костяшке\ будет\ \]

\[хотя\ бы\ один\ нуль:\]

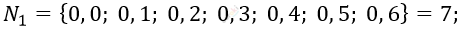
\[m = C_{7}^{2} = \frac{7!}{(7 - 2)! \bullet 2!} = \frac{7!}{5! \bullet 2} =\]

\[= \frac{7 \bullet 6 \bullet 5!}{5! \bullet 2} = 7 \bullet 3 = 21;\]

\[P = \frac{m}{n} = \frac{21}{378} = \frac{7}{126} = \frac{1}{18}\text{.\ }\]