Решебник по алгебре и начала математического анализа 10 класс Алимов Задание 1129

\[\boxed{\mathbf{1129}\mathbf{.}}\]

\[n = 6 \bullet 6 = 36 - число\ всех\ \]

\[возможных\ исходов.\]

\[1)\ на\ обеих\ костях\ выпали\ \]

\[числа\ 6:\]

\[m = \left\{ 6,\ 6 \right\} = 1 - число\ \]

\[благоприятных\ исходов;\]

\[P = \frac{m}{n} = \frac{1}{36}.\]

\[2)\ на\ обеих\ костях\ выпали\ \]

\[числа\ 5:\]

\[m = \left\{ 5,\ 5 \right\} = 1 - число\ \]

\[благоприятных\ исходов;\]

\[P = \frac{m}{n} = \frac{1}{36}.\]

\[3)\ на\ первой\ кости\ выпало\ \]

\[число\ 2,\ а\ на\ второй\ 3:\]

\[m = \left\{ 2,\ 3 \right\} = 1 - число\ \]

\[благоприятных\ исходов;\]

\[P = \frac{m}{n} = \frac{1}{36}.\]

\[4)\ на\ первой\ кости\ выпало\ \]

\[число\ 6,\ а\ на\ второй\ 1:\]

\[m = \left\{ 6,\ 1 \right\} = 1 - число\ \]

\[благоприятных\ исходов;\]

\[P = \frac{m}{n} = \frac{1}{36}.\]

\[5)\ на\ первой\ кости\ выпало\ \]

\[четное\ число,\ а\ на\ второй\ \]

\[число\ 3:\]

\(m = \left\{ 2,\ 3;\ 4,\ 3;\ 6,\ 3 \right\} =\)

\[= 3 - число\ благоприятных\ \]

\[исходов;\]

\[P = \frac{m}{n} = \frac{3}{36} = \frac{1}{12}.\]

\[6)\ на\ первой\ кости\ выпало\ \]

\[число\ 2,\ а\ на\ второй\ нечетное\ \]

\[число:\]

\[m = \left\{ 2,\ 1;\ 2,\ 3;\ 2,\ 5 \right\} =\]

\[= 3 - число\ благоприятных\ \]

\[исходов;\]

\[P = \frac{m}{n} = \frac{3}{36} = \frac{1}{12}.\]

\[7)\ на\ первой\ кости\ выпало\ \]

\[нечетное\ число,\ а\ на\ второй -\]

\[четное:\]

\[N_{1} = \left\{ 1;\ 3;\ 5 \right\} = 3 - вариантов\ \]

\[для\ первой\ кости;\]

\[N_{2} = \left\{ 2;\ 4;\ 6 \right\} = 3 - вариантов\ \]

\[для\ второй\ кости;\]

\[m = N_{1} \bullet N_{2} = 3 \bullet 3 = 9 - число\ \]

\[благоприятных\ исходов;\]

\[P = \frac{m}{n} = \frac{9}{36} = \frac{1}{4}.\]

\[8)\ на\ первой\ кости\ выпало\ \]

\[четное\ число,\ а\ на\ второй -\]

\[кратное\ трем:\]

\[N_{1} = \left\{ 2;\ 4;\ 6 \right\} = 3 - вариантов\ \]

\[для\ первой\ кости;\]

\[N_{2} = \left\{ 3;\ 6 \right\} = 2 - варианта\ для\ \]

\[второй\ кости;\]

\[m = N_{1} \bullet N_{2} = 3 \bullet 2 = 6 - число\ \]

\[благоприятных\ исходов;\]

\[P = \frac{m}{n} = \frac{6}{36} = \frac{1}{6}.\]

\[9)\ на\ первой\ кости\ выпало\ \]

\[число,\ большее\ 2,\ \]

\[а\ на\ второй - число,\]

\[не\ меньше\ 4:\]

\[N_{1} = \left\{ 3;\ 4;\ 5;\ 6 \right\} =\]

\[= 4 - варианта\ для\ первой\ \]

\[кости;\]

\[N_{2} = \left\{ 4;\ 5;\ 6 \right\} = 3 - варианта\ \]

\[для\ второй\ кости;\]

\[m = N_{1} \bullet N_{2} = 4 \bullet 3 =\]

\[= 12 - число\ благоприятных\ \]

\[исходов;\]

\[P = \frac{m}{n} = \frac{12}{36} = \frac{1}{3}.\]

\[10)\ на\ первой\ кости\ выпало\ \]

\[число,\ не\ больше\ 4,\ \]

\[а\ на\ второй - число\ большее\ 4:\]

\[N_{1} = \left\{ 1;\ 2;\ 3;\ 4 \right\} =\]

\[= 4 - варианта\ для\ первой\ \]

\[кости;\]

\[N_{2} = \left\{ 5;\ 6 \right\} = 2 - варианта\ для\ \]

\[второй\ кости;\]

\[m = 4 \bullet 2 = 8 - число\ \]

\[благоприятных\ исходов;\]

\[P = \frac{m}{n} = \frac{8}{36} = \frac{2}{9}.\]

\[11)\ сумма\ выпавших\ чисел\ \]

\[равна\ 3:\]

\[m = \left\{ 1,\ 2;\ 2,\ 1 \right\} = 2 - число\ \]

\[благоприятных\ исходов;\]

\[P = \frac{m}{n} = \frac{2}{36} = \frac{1}{18}.\]

\[12)\ сумма\ выпавших\ чисел\ \]

\[равна\ 4:\]

\[m = \left\{ 1,\ 3;\ 3,\ 1;\ 2,\ 2 \right\} = 3 - число\ \]

\[благоприятных\ исходов;\]

\[P = \frac{m}{n} = \frac{3}{36} = \frac{1}{12}.\]

\[13)\ сумма\ выпавших\ чисел\ \]

\[не\ больше\ 4:\]

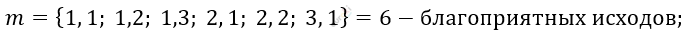
\[P = \frac{m}{n} = \frac{6}{36} = \frac{1}{6}.\]

\[14)\ сумма\ выпавших\ чисел\ \]

\[не\ меньше\ 10:\]

\[P = \frac{m}{n} = \frac{6}{36} = \frac{1}{6}\text{.\ }\]

\[15)\ произведение\ выпавших\ \]

\[чисел\ равно\ 10:\]

\[m = \left\{ 2,\ 5;\ 5,\ 2 \right\} = 2 - число\ \]

\[благоприятных\ исходов;\]

\[P = \frac{m}{n} = \frac{2}{36} = \frac{1}{18}.\]

\[16)\ произведение\ выпавших\ \]

\[чисел\ равно\ 5:\]

\[m = \left\{ 1,\ 5;\ 5,\ 1 \right\} = 2 - число\ \]

\[благоприятных\ исходов;\]

\[P = \frac{m}{n} = \frac{2}{36} = \frac{1}{18}.\]

\[17)\ произведение\ выпавших\ \]

\[чисел\ равно\ 6:\]

\[m = \left\{ 1,\ 6;\ 2,\ 3;\ 3,\ 2;\ 6,\ 1 \right\} = 4 -\]

\[число\ благоприятных\ исходов;\]

\[P = \frac{m}{n} = \frac{4}{36} = \frac{1}{9}.\]

\[18)\ произведение\ выпавших\ \]

\[чисел\ равно\ 4:\]

\[m = \left\{ 1,\ 4;\ 2,\ 2;\ 4,\ 1 \right\} =\]

\[= 3 - число\ благоприятных\ \]

\[исходов;\]

\[P = \frac{m}{n} = \frac{3}{36} = \frac{1}{12}.\]