Решебник по алгебре и начала математического анализа 10 класс Колягин Задание 648

\[\boxed{\mathbf{648}.}\]

\[1)\ y = \frac{3x - 1}{x + 3} = \frac{3x + 9 - 10}{x + 3} =\]

\[= \frac{3(x + 3) - 10}{x + 3} =\]

\[= 3 - \frac{10}{x + 3};x \neq - 3\]

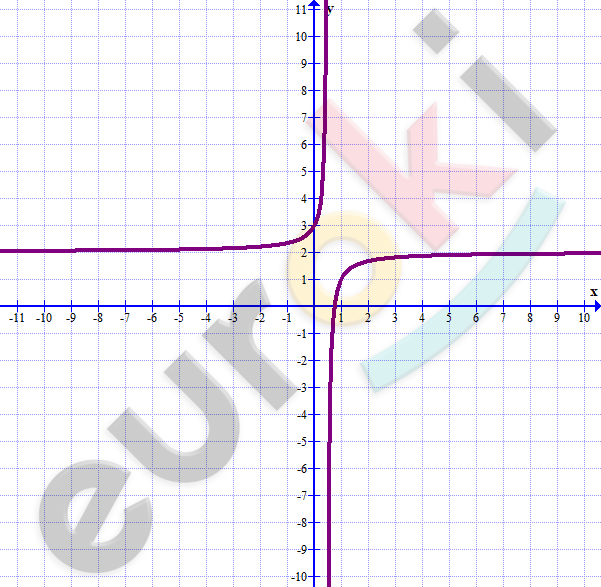
\[2)\ y = \frac{4x - 3}{2x - 1} = \frac{4x - 2 - 1}{2x - 1} =\]

\[= \frac{2 \cdot (2x - 1) - 1}{2x - 1} =\]

\[= 2 - \frac{1}{2x - 1};x \neq 0,5\]

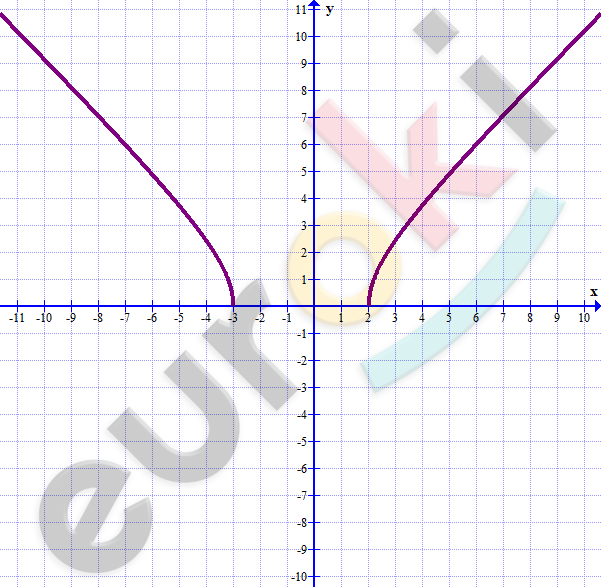
\[3)\ y = \sqrt{(x - 2)(x + 3)}\]

\[(x + 3)(x - 2) \geq 0\]

\[x \leq - 3;\ \ \ x \geq 2\]

\[4)\ y = \sqrt{2x^{2} + 5x - 3}\]

\[2x^{2} + 5x - 3 \geq 0\]

\[D = 25 + 24 = 49\]

\[x_{1} = \frac{- 5 + 7}{4} = \frac{1}{2};\ \]

\[\ x_{2} = \frac{- 5 - 7}{4} = - 3.\]

\[(x + 3)(x - 0,5) \geq 0\]

\[x \leq - 3;\ \ x \geq 0,5.\]

\[5)\ y = \frac{1}{(x + 1)(x + 2)};\ \ \]

\[x \neq - 1;\ \ x \neq - 2.\]

\[6)\ y = \frac{1}{x^{2} - 7x - 8}\]

\[x^{2} - 7x - 8 \neq 0\]

\[x_{1} + x_{2} = 7;\ \ \ x_{1} \cdot x_{2} = - 8\]

\[x_{1} \neq 8;\ \ \ x_{2} \neq - 1.\]