Решебник по алгебре и начала математического анализа 10 класс Колягин Задание 306

\[\boxed{\mathbf{306}.}\]

\[P(x) = 6x^{3} + bx^{2} - 5x - 2;\]

\[\ \ x = - \frac{1}{2}:\]

\[P\left( - \frac{1}{2} \right) = 6 \cdot \left( - \frac{1}{8} \right) + \frac{1}{4}b - \frac{5}{2} -\]

\[- 2 = - \frac{3}{4} + \frac{1}{4}b - \frac{10}{4} - 2 =\]

\[= \frac{1}{4}b - \frac{1}{4}\]

\[\frac{1}{4}b - \frac{1}{4} = 0\]

\[b = 1.\]

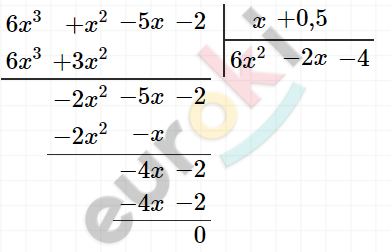
\[6x^{2} - 2x - 4 = 0\ \ \ |\ :2\]

\[3x^{2} - x - 2 = 0\]

\[D = 1 + 24 = 25\]

\[x_{1} = \frac{1 + 5}{6} = 1;\ \ \]

\[x_{2} = \frac{1 - 5}{6} = - \frac{4}{6} = - \frac{2}{3}.\]

\[Ответ:x = - \frac{2}{3};\ - \frac{1}{2};\ \ 1.\]